Esercitazione Econometria

Console online

Dati Statistici tratti dal sito ufficiale dell'ISTAT Dati Statistici tratti dal sito ufficiale dell'EUROSTAT

Dati Statistici tratti dal sito ufficiale della Banca d'Italia Dati Statistici tratti dal sito ufficiale dell'OCSE

Per personalizzare gli scripts con dati propri oppure importati dai siti sopra riportati

l'Utente può utilizzare la seguente R Console online Interattiva

PROVA IN ITINERE DI ECONOMETRIA DEL 27/02/2019 DIPARTIMENTO DI ECONOMIA UNIVERSITA’ DI FOGGIA

Domande a risposta multipla (quattro risposte di cui una sola corretta)

1) Quale è la notazione con cui si calcola il Chi-quadrato semplice:

a) Chi-quadr=∑_r∑_ccont. ass.²/freq. teor

b) Chi-quadr=∑_r conr ass.²/freq. teor

c) Chi-quadr=∑_cconr ass.²/freq. teor

d) Chi-quadr=∑_r∑_cconr ass./freq. teor

2) Quale è la notazione con cui si calcola il Chi-quadrato max:

a) Chi-quadr max=N*max(r-1)(c-1)

b) Chi-quadr max=N*min(r-1)(c-1)

c) Chi-quadr max=N*max(r-1)(c)

d) Chi-quadr max=N*min(r)(c-1)

3) Quale è la notazione con cui si calcola il Chi-quadrato normalizzato

a) Chi-quadr norm= Chi-quadr* Chi-quadr max

b) Chi-quadr norm= Chi-quadr-Chi-quadr max

c) Chi-quadr norm= Chi-quadr/Chi-quadr max

d) Chi-quadr norm= Chi-quadr+ Chi-quadr max

4) Quando si può affermare che il carattere inflazione Italia è dipendente dal carattere inflazione GERMANIA:

a) Basta che una frequenza teorica differisca dalla relativa frequenza congiunta assoluta

b) Basta che una frequenza teorica non differisca dalla relativa frequenza congiunta assoluta

c) Basta che una frequenza teorica sia uguale alla relativa frequenza congiunta assoluta

d) Basta che una frequenza teorica risulti il doppio della relativa frequenza congiunta assoluta

5) Con quale linea di codice si calcola il quantile della t critica per un test bilatero con un livello di significatività alfa=0.05 con 11 gradi di libertà:

a) t_critica<-qt(1-0.05/2,11);t_critica

b) t_critica<-qt(1-0.05,11);t_critica

c) t_critica<-qt(0.05,11);t_critica

d) t_critica<-qt(1-0.05,11);t_critica

6) Con quale linea di codice si calcola la statistica t di Student empirica:

a) t<-(media_camp-mu)*sqrt(n)/sqm;t

b) t<-(media_camp-mu)/sqm;t

c) t<-(media_camp-mu)*sqrt(n)/;t

d) t<-(media_camp)*sqrt(n)/sqm;t

7) Con quale notazione si calcola il coefficiente angolare stimato nel MRLS con il metodo dei minimi quadrati:

a) b(stim)=cov(XY)/var(X)

b) b(stim)=cov(X)/var(X)

c) b(stim)=cov(XY)/var(Y)

d) b(stim)=cov(XY)/dev(X)

8) Con quale notazione si calcola l’intercetta stimata nel MRLS con il metodo dei minimi quadrati:

a) a(stim)= Y(media)-b*X

b) a(stim)= Y(media)-b*X(media)

c) a(stim)= Y-b*X(media)

d) a(stim)= Y(media)-X(media)

9) Con quali linee di codice si ottiene l’output della regressione lineare semplice con R:

a) modello<-(y~x); summary(modello)

b) modello<-lm(y~x); summary(modello)

c) modello<-lm(y~x); summary

d) modello<-lm(y+x); summary(modello)

10) Con quale linea di codice si calcola il quantile della F critica per un test bilatero con un livello di significatività alfa=0.05 con 11 gradi di libertà al numeratore e 15 al denominatore:

a) F_critica<-qf(1-0.05/2,11,15);F_critica

b) F_critica<-qf(1-0.05, 11,15);F_critica

c) F_critica<-qf(0.05, 11,15);F_critica

d) F_critica<-qf(1-0.05, 11,15);F_critica

11) Con quali linee di codice si calcolano i p-value, dati i valori dei quantili empirici della t di Student pari a -2.228 e 1,23, per un test bilatero con 11 gradi di libertà:

a) p-value<-(pt(-2.228,11));p_value - p-value<-(1-pt(1.23, 11));p_value

b) p-value<-2*(pt(-2.228,11));p_value - p-value<-2*(1-pt(1.23, 11));p_value

c) p-value<-2*(pt(-2.228));p_value - p-value<-2*(1-pt(1.23,));p_value

d) p-value<-2*(pt(-2.228,11));p_value - p-value<-2*(pt(1.23, 11));p_value

Domande a risposta aperta.

1. Da una indagine statistica bivariata sono stati rilevati i seguenti dati 0, 0, 1, 2, 3, 2, 1,2, 2 del carattere X che assume le modalità (alto,medio,basso) e del carattere Y che assume le modalità (1,2,3) e si vuole: a) implementare il codice per costruire la relativa matrice; b) redigere la tabella a doppia entrata delle frequenze congiunte assolute; c) redigere la tabella a doppia entrata delle frequenze teoriche; d) redigere la tabella a doppia entrata delle contingenze assolute.

2. Con gli stessi dati della domanda 3 si vuole: a) redigere la tabella a doppia entrata delle contingenze assolute al quadrato diviso le frequenze teoriche; b) calcolare il chi-quadrato semplice; c) calcolare il chi-quadrato massimo; d) calcolare il chi-quadrato normalizzato e svolgere un breve commento.

3.(Microeconometria). Si vuole studiare la relazione tra i ricavi di intermediazione bancaria Y e il numero dei dipendenti X e allo scopo sono state rilevate le seguenti coppie di valori i: (10;255-11;365-14;485-18;592-25) e si vuole calcolare: a) l'intercetta stimata; b) il coefficiente angolare; c) l’equazione della retta stimata; d) il valore dei ricavi di intermediazione bancaria stimati, per un valore del numero di dipendenti pari a 22 e un breve commento.

4.(Microeconometria). Con gli stessi dati dell’esercitazione 3 si vuole implementare: a) il codice di R per la relazione della retta stimata fra Y ed X; b) il codice per il calcolo dei coefficienti di regressione; c) il codice per il calcolo dei residui di regressione; d) il codice per l’output della regressione.

5.(Macroeconometria). Con gli stessi dati dell’esercitazione 3 si vuole implementare: a) il codice di R per il calcolo della t empirica dell’intercetta; b) il codice di R per il calcolo della t empirica del coefficiente angolare; c) il codice di R per il calcolo del p-value dell’intercetta; d) ) il codice di R per il calcolo del p-value del coefficiente angolare.

#########################################################################

PROVA IN ITINERE DI ECONOMETRIA DEL 13/03/2019 DIPARTIMENTO DI ECONOMIA UNIVERSITA’ DI FOGGIA

SOLUZIONI RISPOSTE CHIUSE: 1 (a), 2(a), 3(a), 4(a), 5(a), 6(c), 7(a), 8(b), 9(a), 10(b), 11(d)

Sezione 2 – Domande a risposta aperta

Domanda aperta 1. Dati i seguenti valori di output di R:

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 2195.5128 1391.6312 ……… 0.1387

x1 18.4367 20.7369 ……… 0.3901

x2 1.9103 0.9344 ……… 0.0617 .

calcolare: a) i valori mancanti dei tre t-value; b) le linee di codice di R per controllare che il calcolo manuale sia corretto sapendo che n=16 e la linea di codice per il calcolo del p-value dell’intercetta e del coefficiente angolare; c) impostare il sistema di ipotesi complesso per i due coefficienti angolari di x1 e x2 per un test bilatero e scegliere la regola di decisione prendendo a riferimento i valori della t empirica e della t critica, al livello di significatività del 5%, pari a 2,16 (della quale si deve indicare la linea di codice di R per ottenerla) presentando la relativa rappresentazione grafica e svolgere un sintetico commento; d) controllare la regola di decisione ottenuta implementando la tecnica del p-value e svolgere un sintetico commento.

SOLUZIONE: punto a) i valori mancanti dei tre coefficienti di regressione sono rispettivamente: (2195.5128/1391.6312)=1.578; (18.4367/20.7369)=0.889: (1.9103/0.9344)=0.0617; punto b) prima di scrivere le linee di codice è opportuno precisare che i coefficienti di regressione di distribuiscono secondo un v.c. continua t di Student con n-k gradi di libertà dove k sono le due covariate più l’intercettale e quindi df=16-3=13; esse saranno rispettivamente: qt(1-0.1387/2,13); qt(1-0.3901/2,13); qt(1-0.0617/2,13); punto c) i sistema di ipotesi complesso per i coefficienti angolari della x1 e della x2 è il seguente: H₀: b₁ , b₂ =0 vs H₀: b₁ , b₂ ≠ 0; per scegliere la regola di decisione ovvero se accettare o rifiutare l’ipotesi nulla occorre presentare la curva della v.c. continua t di Student indicando le regioni di rifiuto e di accettazione:

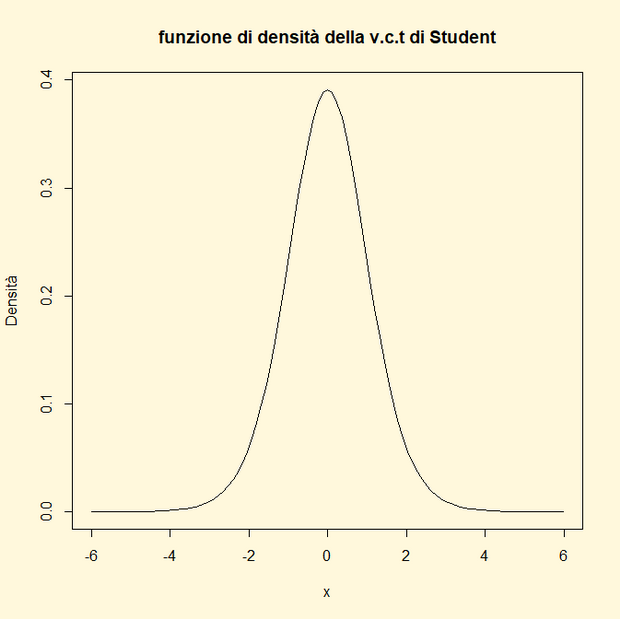
-t_critica=- 2,16 +t_critica= +2,16

poiché i valori delle t empiriche dei coefficienti angolari di x1 e x2 sono ricompresi fra -2,16 e 2,16 si accetta l’ipotesi nulla ovvero non esiste statisticamente una relazione lineare tra le covariate x1 e x2 e la variabile dipendente y; la linea di codice per calcolare il valore della t critica negativa al livello di significatività del 5% per un test bilatero è la seguente: qt(0.025,13) mentre per la t critica positiva è: qt((1-0.025),13); punto d) per controllare la regola di decisione scelta si implementa la tecnica del p-value; si mette a confronto il valore del livello di significatività per un test bilatero pari a 0,05/2=0,025 e i valori delle probabilità delle due t empiriche (p-value); dai dati della domanda appare chiaro che sia 0.3901 che 0.0617 sono entrambi maggiori di 0,025 per cui è confermata l’accettazione dell’ipotesi nulla.

Domanda aperta 2. Data i valori delle covariate x1 e x2 (6.5,6.8,7.1,5.4,5.9,5.1,2.1,2.4,2.8,2.9,2.4,2.3) e i valori della variabile dipendente (1212,1314,1116,1242,1306,1278) riferiti a 6 osservazioni campionarie: a) quali sono le linee di codice per calcolare la matrice X_6x3, la sua trasposta e il prodotto delle due; b) quali sono le linee di codice per calcolare l’inversa e la verifica che essa sia invertibile; c) quale linea di codice si implementa per calcolare il vettore della variabile dipendente y; d) scrivere la formula per il calcolo del vettore dei parametri e l’insieme dei codici per calcolarlo ed inoltre effettuare il controllo manuale e quello del codice con cui ottenere l’output della regressione da cui emerge se il calcolo effettuato è corretto.

SOLUZIONE:

punto a) le linee di codice sono le seguenti:

X <- matrix (data =c(1,1,1,1,1,1,6.5,6.8,7.1,5.4,5.9,5.1,2.1,2.4,2.8,2.9,2.4,2.3), nrow = 6, ncol = 3);X

XT<-t(X);XT

XTX<-XT%*%X;XTX

dove XT sta per trasposta di X

punto b) le linee di codice sono le seguenti:

XTXINV<-solve(XTX);XTXINV

round(XTXINV%*%XTX)

dove XTXINV sta per l’inversa del prodotto tra la trasposta di X e X

punto c) le linee di codice sono le seguenti:

Y <- matrix (data =c(1212,1314,1116,1242,1306,1278),nrow = 6, ncol = 1);Y

punto d) la formula per il calcolo del vettore dei parametri in forma matriciale è la seguente: b(stim)=(X’X)^-1X’y e le linee di codice per calcolarlo sono le seguenti:

X <- matrix (data =c(1,1,1,1,1,1,6.5,6.8,7.1,5.4,5.9,5.1,2.1,2.4,2.8,2.9,2.4,2.3), nrow = 6, ncol = 3);X

XT<-t(X);XT

XTX<-XT%*%X;XTX

XTXINV<-solve(XTX);XTXINV

round(XTXINV%*%XTX)

y <- matrix (data =c(1212,1314,1116,1242,1306,1278),nrow = 6, ncol = 1);y

bstim<-XTXINV%*%XT%*%y;bstim

Per quanto riguarda il controllo manuale si procede come segue: la matrice X è (6x3); la sua trasposta X’ è (3x6); il prodotto di X’(3x6)*X(6x3) è una matrice(3x3); la sua inversa è sempre una (3x3); il prodotto di (X’X)^-1(3x3) per X’(3x6) è una matrice(3x6);il vettore y(6x1), infine il prodotto della matrice risultato (3x6) e il vettore y (6x1) dà un vettore (3x1) che è quello calcolato.

Per quanto riguarda i codici con cui si implementa la regressione in questione che permettono di verificare la correttezza del calcolo del vettore dei parametri essi sono:

y<-c(1212,1314,1116,1242,1306,1278)

x1<-c(6.5,6.8,7.1,5.4,5.9,5.1)

x2<-c(2.1,2.4,2.8,2.9,2.4,2.3)

modello<-lm(y~x1+x2); summary(modello

)

Domanda aperta 3. Dati i seguenti valori di y(1212,1314,1116,1242,1306,1278), x1(6.5,6.8,7.1,5.4,5.9,5.1), x2(2.1,2.4,2.8,2.9,2.4,2.3). Effettuando la regressione lineare multipla con R si ottiene il seguente output (una parte del tutto):

Residual standard error: 75.12 on 3 degrees of freedom

Multiple R-squared: 0.3801, Adjusted R-squared: -0.03318

F-statistic: 0.9197 on 2 and 3 DF, p-value: 0.4881

Descrivere: punto a) la formula con cui si calcola Multiple R-squared e Adjusted R-squared (coefficiente di determinazione semplice e aggiustato), le linee di codice per calcolarli e svolgere un sintetico commento su valore 0.3318; punto b) impostare il sistema per verificare l’ipotesi di linearità del modello per un test bilatero e scegliere la regola di decisione prendendo a riferimento i valori della F empirica e della F critica (0.02553268: 16.04411), al livello di significatività del 5% (della quale si deve indicare le linee di codice di R per ottenerle); punto c) presentare la relativa rappresentazione grafica e svolgere un sintetico commento; punto d) controllare la regola di decisione ottenuta implementando la tecnica del p-value e svolgere un sintetico commento.

SOLUZIONE: punto a) la formula per il calcolo del coefficiente di determinazione semplice è: R²=1- (DR/DT) dove DR è la somma dei quadrati dei residui (devianza residua) [yi-y(stim)]²e DT la somma dei quadrati del totale (devianza totale) ) [yi-y(medio)]²; la formula per il calcolo del coefficiente di determinazione aggiustato é. R²(adj)= 1- (DR/DT)(n-1)/(n-k-1) dove n sono il numero di osservazioni campionarie e k il numero di covariate; le linee di codice sono le seguenti:

y<-c(1212,1314,1116,1242,1306,1278)

x1<-c(6.5,6.8,7.1,5.4,5.9,5.1)

x2<-c(2.1,2.4,2.8,2.9,2.4,2.3)

res<-lm(y~x1+x2);res

summary(res)

mean(y)

n<-6

k<-2

ystim<-1749.47-42.74*x1-97.72*x2;ystim

DT<-sum((y-mean(y))^2);DT

DR<-sum((y-ystim)^2);DR

DS<-sum((ystim-mean(y))^2);DS

R2<-1-(DR/DT);R2

R2adj<-1-((DR/DT)*(n-1)/(n-k-1));R2adj

Per quanto riguarda il valore del coefficiente di determinazione semplice esso esprime una basso adattamento ai dati e quindi la bontà del modello è scarsa e non si possono fare stime previsionali attendibili.

punto b)e c) il sistema di ipotesi è: H0: non linearità vs H1: linearità

Per testare tale ipotesi si utilizza la statistica-test F di Fisher. Il valore che restituisce R è estremamente basso. Per decidere se accettare o rifiutare l’ipotesi nulla si mette a confronto il valore della F empirica con quello della F critica

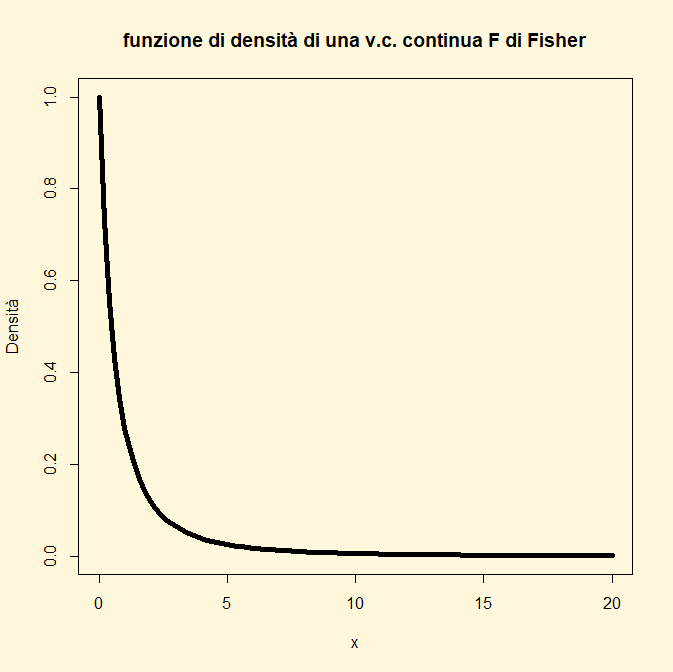
Fcritica=0.025 Fempirica=0.9197 Fcritica=16.04

Dal grafico si evince chiaramente che la F empirica cade nella regione di accettazione per cui si accetta che l’ipotesi di linearità non è statisticamente rispettata. Le linee di codice per ottenere i valori della F critica sono:

qf(0.025,2,3)

qf((1-0.025),2,3)

punto d) per controllare la regola di decisione scelta si implementa la tecnica del p-value; si mette a confronto il valore del livello di significatività per un test bilatero pari a 0,05/2=0,025 e il valore della probabilità della F empirica (p-value); dai dati della domanda emerge che esso è pari a 0.4881>0.025 per cui è confermata l’accettazione dell’ipotesi nulla.

Domanda aperta 4. Con i dati della domanda 3 spiegare: a) i concetti sulla multicollinearità; b) la differenza fra multicollinearità perfetta ed imperfetta; c) gli indicatori più importanti che segnalano la presenza o l’assenza di multicollinearità, la scala di misurazione e la linea di codice; d) i rimedi per risolvere eventuali problemi di multicollinearità.

punto a) è opportuno premettere che la multicollinearità testa la verifica dell’ipotesi di correlazione fre le covariate; poiché la stima del vettore dei parametri nel MRLM è possibile solo se esiste la matrice (X’X)^-1 e quindi la matrice di varianze-covarianze X’X deve essere invertibile e per essere tale deve avere rango pieno e un determinante diverso da zero e le covariate non debbono essere tra loro correlate; qualora invece essere fossero correlate il determinante della matrice di varianze-covarianze X’X si approssimerebbe 0 e si avrebbe un vettore dei parametri sovra dimensionato che genera multicollinearità.

punto b) la multicollinearità perfetta si determina quando una o più di una covariata è perfetta combinazione lineare di un’altra; in questo caso la matrice X è una matrice singolare, la quale può essere definita come una matrice quadrata con determinante uguale a zero, oppure, analogamente, una matrice quadrata il cui rango non è massimo; con l’assunto che nessuna matrice singolare è invertibile; pertanto non è definita la matrice (X’X)^-1

punto c) gli indicatori più importanti sono: il coefficiente di determinazione semplice R²; il coefficiente di tolleranza t= 1- R²; il VIF (Variance Inflation Factor)=1/(1- R²); la matrice di correlazione fra le covariate. Per quanto riguarda i primi tre indicatori è superfluo ogni commento in quanto da soli esprimono il significato; per quanto riguarda la matrice di correlazione fra le covariate può essere interessante riprendere due codici di R: il primo che dà il valore del coefficiente di correlazione fra la x1 e x2 e il secondo che restituisce la matrice di correlazione:

cor(x1,x2)

[0.01093713]

X <- matrix (data =c(6.5,6.8,7.1,5.4,5.9,5.1,2.1,2.4,2.8,2.9,2.4,2.3), nrow = 6, ncol = 2); cor(X)

[,1] [,2]

[1,] 1.00000000 0.01093713

[2,] 0.01093713 1.00000000

dove il valore 1 esprime la correlazione fra una covariata e se stessa (x1,x1) e (x2,x2) per i=j mentre 0,01093713 la correlazione fra una e l’altra per i≠j; la scala di misurazione consigliata per i valori di VIF è la seguente: superiori a 20 forte presenza; tra 7 e 20 prenza media ma in crescita; inferiori a 7 sostanziale assenza

punto d) per tentare di risolvere eventuali problemi di multicollinearità si può cercare di far divenire la matrice X arango pieno aumentando il numero di osservazioni; oppure rimuovere le covariate correlate ed utilizzare le tecniche della principal component regression o ridge regression.

Domanda aperta 5. Dato un MRLM spiegare: a) i concetti sulla omoschedasticità ed eteroschedasticità degli errori e quali sono gli strumenti per individuarla; b) quando viene meno l’ipotesi omoschedasticità il vettore dei parametri quali proprietà assume; c) quale sistema di ipotesi si imposta e quali test si utilizzano per verificare la presenza o l’assenza di eteroschedasticità; d) come si distribuisce il test BP per K=3 e come si rappresentano graficamente le regioni di rifiuto e di accettazione per un test bilatero ad un livello di significatività del 5% e quali linee di codice si utilizzano per scegliere la regola di decisione tenuto conto che la chi-quad empirica è pari a .

punto a) per omoschedasticità si intende che la varianza degli errori del modello è costante; per eteroschedasticità si intende invece che la varianza non è costante; gli strumenti per individuarla sono lo studio dei grafici e l’analisi di appositi test;

punto b) quando viene meno l’ipotesi omoschedasticità degli errori il vettore dei parametri rimane corretto e non distorto ma non è più asintoticamente efficiente ovvero non ha la più bassa varianza;

punto c) i sistema di ipotesi da impostare è il seguente: H=:assenza di eteroschedasticità vs H1: presenza di eteroschedasticità; i test che si possono utilizzare sono: di White; di Goldfeld-Quandt; di Breusch-Pagan e Non costant Variance (NCV);

punto d) il test BP si distribuisce secondo una Chi-quadrato con k-1 gradi di libertà (nel nostro caso 3-1=2); le linee di codice per calcolare la Chi-quadrato critica per un test bilatero al livello di significatività del 5% sono:

qchisq(0.025,2)

qcisq((1-0.025),2)

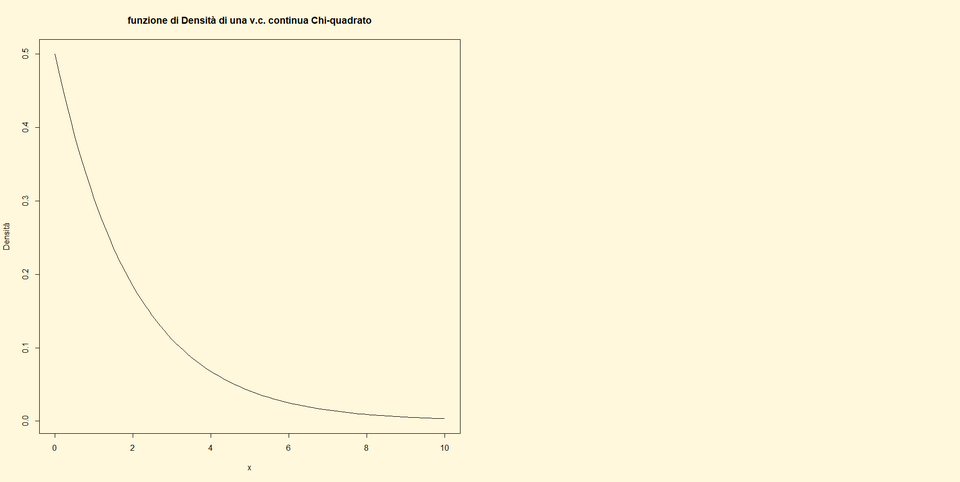
Chi-quadr critica=0.05 Chi-quadr empirica =0.9197 Chi-quadr critica =7.38

##############################################################

UNIVERSITA’ DEGLI STUDI DI FOGGIA DIPARTIMENTO DI ECONOMIA

Esercitazione di ECONOMETRIA svolta

del 17.04/2019

Prof. Raoul COCCARDA

Sezione 1 – Domande a risposta multipla

1) Quale linea di codice di R si utilizza per calcolare gli indicatori C,alpha e DG.rho in un modello di regressione a variabili latenti per il data frame df

library(“plspm”); satpls<-plspm(df,sat.inner,sat.outer,sat.mod, scheme=”centroid”;scaled=TRUE) (satpls) a

library(“plspm”); satpls<-plspm(df,sat.inner,sat.outer,sat.mod, scheme=”centroid”) summary(satpls) b

library(“plspm”); satpls<-plspm(df,sat.inner,sat.outer,sat.mod, scaled=TRUE) summary(satpls) c

library(“plspm”); satpls<-plspm(df,sat.inner,sat.outer,sat.mod, scheme=”centroid”;scaled=TRUE) summary(satpls) d

2) Entro quale intervallo di valori varia l’indicatore DG.rho:

tra 0 ed 1 a

tra 0 ed 2 b

tra 1 ed 2 c

tra 1 ed 3 d

3) Sia svolta un’analisi semplice bayesiana com probabilità a priori pari a 1/3 su tre opzioni oro-oro, oro-argento, argento-argento. Se si suppone di estrarre un gioiello d’oro quale è probabilità a posteriori P(oro-argento|oro)

0,1 a

0,33 b

0 c

1.1 d

4) Come può essere la probabilità a priori.

Informativa – Non informativa o di Jeffreys a

Informativa b

Non Informativa c

Nulla d

5) Come può essere la probabilità a priori informativa

Coniugata a

Non coniugata b

Coniugata e non coniugata c

Diretta d

6) Quale è l’equazione del modello logistico

Y=µ-є a

Y=µ(x)+є b

Y=µ(x) c

Y= µ(x)*є d

7) Quale è l’equazione del modello logit

logit[µ(x)]=ln[µ(x) /1- µ(x)] a

logit[µ(x)]=[µ(x) /1- µ(x)] b

logit[µ(x)]=ln[µ(x) *1- µ(x)] c

logit[µ(x)]=ln[µ(x) +1- µ(x)] d

8) Data una variabile dipendente dicotomica y e due covariate x1 e x2 quali linee di codice si implementano

per calcolare il modello logit definito semplicemente modello

modello<-lm(y~x1+x2, family=binomial;summary(modello) a

modello<-lm(y~x1+x2, family=(link=logit));summary(modello) b

modello<-glm(y~x1+x2,family=binomial(link=logit)));summary(modello) c

modello<-glm(y~x1*x2,family=binomial(link=logit)));summary(modello) d

9) Solitamente quando si utilizza il modello di regressione robusto

Quando, attraverso un’opportuna diagnostica, si individua la presenza di valori anomali (outliers) a

Quando si individua la presenza di valori anomali (outliers) b

Quando, attraverso un’opportuna diagnostica, si individua l’assenza di valori anomali (outliers) c

Quando, attraverso un’opportuna diagnostica, si verifica la presenza di valori mancanti d

10) Quale funzione prende in considerazione il modello probit

La funzione di ripartizione della t di Student a

La funzione di ripartizione della t di Student b

La funzione di ripartizione della t di Student c

La funzione di ripartizione della v.c. normale standardizzata d

11) Data una variabile dipendente dicotomica y e due covariate x1 e x2 quali linee di codice si implementano

per calcolare il modello logit definito semplicemente modello

modello<-lm(y~x1+x2, family=binomial;summary(modello) a

modello<-lm(y~x1+x2, family=(link= probit));summary(modello) b

modello<-glm(y~x1+x2,family=binomial(link= probit)));summary(modello) c

modello<-glm(y~x1*x2,family=binomial(link=probit)));summary(modello) d

SOLUZIONI RISPOSTE CHIUSE: 1 (d), 2(a), 3(b), 4(a), 5(c), 6(b), 7(a), 8(c), 9(a), 10(d), 11(d)

Sezione 2 – Domande a risposta aperta

Domanda aperta 1. Dato il seguente data frame che contiene sulle righe le 5 unità statistiche osservate e sulle colonne i valori delle due covariate x1, x2, dell’l’intercetta o costante e della variabile dipendente Y:

interc. x1 x2 Y

1 1 12 48 128

2 1 13,5 44 132

3 1 11,8 40,7 164

4 1 9,2 36,1 181

5 1 8,5 29,9 177

presentare: a) le formule del vettore dei parametri, del coefficiente di determinazione R² e di correlazione R in forma compatta (o matriciale), della scomposizione della devianza e i relativi calcoli manuali; b) le linee di codice di R per controllare che il calcolo manuale sia corretto; c) le linee di codice per implementare il modello e il relativo output; d) impostare il sistema di ipotesi complesso per i due coefficienti angolari di x1 e x2 per un test bilatero e scegliere la regola di decisione prendendo a riferimento i due metodi, tenuto conto di un livello di significatività del 5%, pari a 2,16 (della quale si deve indicare la linea di codice di R per ottenerla) presentando la relativa rappresentazione grafica e svolgere un sintetico commento.

SOLUZIONE: punto a) assumendo che X è una matrice 5x3, che X’ è una matrice 3x5, che il prodotto di X’(3x5) X(5x3) è una matrice 3x3; che l’inversa [X’(3x5) X(5x3)]^-1 dà una matrice (3x3); che y è un vettore (5x1) la formula per il calcolo del vettore dei parametri è:

b(stim)(3x1)= [X’(3x5) X(5x3)]^-1_(3x3) [X’(3x5)y(5x1)] _(3x1)

Dato che per definizione la formula per il calcolo del vettore il coefficiente di determinazione è uguale a 1-DR/DT, che in forma matriciale si trasforma in: 1- [e’e/y’y-ny²(media)] in quanto in forma matriciale DR= y’y-β(stim)XX’ β(stim) e DT=∑_t[(y_t-y(media)]²= y’y-ny²(media)] utilizzando la notazione operativa; che il numeratore e’e , utilizzando la notazione operativa diventa [β’(stim) X’X] β(stim)] la formula è:

numeratore R²=[(β’(stim)_1x3 X’X_3x3] β(stim)_3x1)- ny²(media)]_1x1(scalare)

denominatore R²=[y_5x1 y’_x51- ny²(media)]_1x1(scalare)

R²=(numeratore)/(denominatore)

(Lo studente deve svolgere i calcoli manuali)

punto b) Le linee di codice di R per i calcoli di cui al punto a) sono:

X<-matrix(data=c(1,1,1,1,1,12,13.5,11.8,9.2,8.5,48,44,40.7,36.1,29.9),nrow=5,ncol=3);X

D<-t(X);D ##matrice trasposta

C<-D%*%X;C ## prodotto XX’

N<-solve (C);N ## matrice inversa

round(C%*%N) ## controllo che il risultato restituisca la matrice identità

Y<- matrix(data=c(128, 132, 164,181,177),nrow=5,ncol=1);Y ##vettore della Y

E<-D%*%Y;E ## prodotto X’Y

M<- N%*%E;M ## vettore dei parametri β(stim)

n<-5

y<-c(128, 132, 164,181,177)

m<-mean(y)

A<-(t(M)%*%C%*%M)-n*m^2;A ## numeratore del coefficiente di determinazione

B<-( t(Y)%*%Y)-n*m^2;B ## denominatore del coefficiente di determinazione

R<- A/B;R ## coefficiente di determinazione

Rho<-sqrt(R);Rho ## coefficiente di correlazione

########################################################

punto c) Le linee di codice di R per ottenere l’output sono:

y<-c(128, 132, 164,181,177)

x1<-c(12,13.5,11.8,9.2,8.5)

x2<-c(48,44,40.7,36.1,29.9)

modello<-lm(y~x1+x2); summary(modello)

Il relativo output che R restituisce si riporta di seguito:

Call:

lm(formula = y ~ x1 + x2)

Residuals:

1 2 3 4 5

-7.178 -4.882 13.021 9.375 -10.336

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 285.243 42.811 6.663 0.0218 *

x1 -4.320 7.158 -0.604 0.6075

x2 -2.046 2.124 -0.963 0.4370

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 14.83 on 2 degrees of freedom

Multiple R-squared: 0.8234, Adjusted R-squared: 0.6468

F-statistic: 4.662 on 2 and 2 DF, p-value: 0.1766

(Si consiglia lo studente di utilizzare la RConsole libera presente nell’area riservata del sito: www.didatticainterattiva.it per verificare gli script e controllare che i valori siano corretti)

punto d) i sistema di ipotesi complesso per i coefficienti angolari della x1 e della x2 è il seguente: H₀: β₁ =β₂ =0 vs H₀: β₁ ≠ β₂ ≠ 0; per scegliere la regola di decisione con il metodo del confronto fra la t critica e quella empirica occorre presentare la curva della v.c. continua t di Student indicando le regioni di rifiuto e di accettazione:

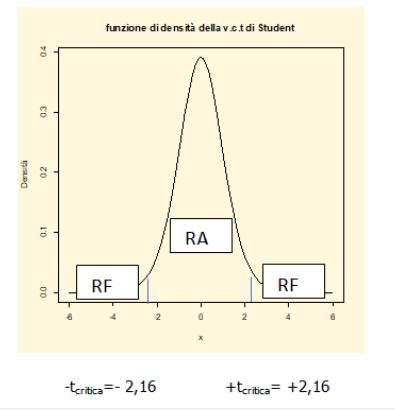
poiché i valori delle t empiriche dei coefficienti angolari di x1 e x2 sono ricompresi fra -2,16 e 2,16 si accetta l’ipotesi nulla ovvero non esiste statisticamente una relazione lineare tra le covariate x1 e x2 e la variabile dipendente y; la linea di codice per calcolare il valore della t critica negativa al livello di significatività del 5% per un test bilatero è la seguente: qt(0.025,13) mentre per la t critica positiva è: qt((1-0.025),13); per controllare la regola di decisione scelta con la tecnica del p-value si mette a confronto il valore del livello di significatività per un test bilatero pari a 0,05/2=0,025 e i valori delle probabilità delle due t empiriche (p-value); dai dati della domanda appare chiaro che sia 0.6075 che 0.4370 sono entrambi maggiori di 0,025 per cui è confermata l’accettazione dell’ipotesi nulla.

Domanda aperta 2. Si esaminano i bilanci di 5 banche, si estraggono i seguenti dati e si assume che: le commissioni attive in ML di Euro (punto 50 del conto economico) esprimono la variabile dipendente y (10, 11, 13, 15, 9); le spese del personale [punto 150 a) del conto economico] variabile indipendente x1 (0,4-0,39-0,45-0,65-0,28); altre spese amministrative [ punto 150 b) del conto economico] variabile indipendente x2 (0,11-0,12-0,15-0,09-0,08) : punto a) commentare brevemente come si procede alla specificazione del modello, quali notazioni si utilizzano sia in forma analitica che compatta e quali linee di codice si eseguono per calcolare l’output; punto b) implementando il modello si ottiene il seguente output di R:

Call:

lm(formula = y ~ x1 + x2)

Residuals:

1 2 3 4 5

-1.03300 -0.03844 0.44435 0.14229 0.48479

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 2.468 2.237 1.103 0.3849

x1 16.676 3.214 5.189 0.0352 *

x2 17.221 15.932 1.081 0.3928

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8721 on 2 degrees of freedom

Multiple R-squared: 0.9344, Adjusted R-squared: 0.8689

F-statistic: 14.25 on 2 and 2 DF, p-value: 0.06557

svolgere un’analisi diagnostica sull’ipotesi di correlazione fra le covariate (multicollinearità) utilizzando gli strumenti studiati ed implementando le linee di codice di R per calcolarli.

punto c) introducendo una nuova covariata x3 rappresentata dal margine di intermediazione (punto 120 del conto economico) che presenta i seguenti dati (1,1-1,3-0,9-1,0-0,7) implementando il modello1 si ottiene il seguente output:

Call:

lm(formula = y ~ x1 + x2 + x3)

Residuals:

1 2 3 4 5

-0.83051 0.48416 0.06566 0.09525 0.18544

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 3.471 2.859 1.214 0.439

x1 17.329 3.735 4.639 0.135

x2 21.919 19.063 1.150 0.456

x3 -1.803 2.398 -0.752 0.590

Residual standard error: 0.9859 on 1 degrees of freedom

Multiple R-squared: 0.9581, Adjusted R-squared: 0.8324

F-statistic: 7.623 on 3 and 1 DF, p-value: 0.2588

Verificare se la covariata aggiunta x3 contribuisce in modo significativo ad aumentare il potere esplicativo del modello; mostrare che la statistica F calcolata è esattamente uguale al quadrato della statistica t di Student;

punto d) “droppando” ovvero eliminando dal modello la covariata x2, rappresentata dalle altre spese amministrative) si implementa il modello2 e si ottiene il seguente output:

Call:

lm(formula = y ~ x1 + x3)

Residuals:

1 2 3 4 5

-0.9275 0.4236 1.0360 -0.3011 -0.2309

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 5.0624 2.6955 1.878 0.2011

x1 17.1347 4.0208 4.261 0.0509 .

x3 -0.8989 2.4411 -0.368 0.7480

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.062 on 2 degrees of freedom

Multiple R-squared: 0.9027, Adjusted R-squared: 0.8054

F-statistic: 9.279 on 2 and 2 DF, p-value: 0.09728

Verificare se la covariata eliminata x2 contribuisce in modo significativo ad aumentare il potere esplicativo del modello.

SOLUZIONE: punto a) la notazione in forma analitica del modello è la seguente: y= β₀+ β₁ x₁ + x₂ β₂ + є mentre in forma compatta Y_(nx1)= βX_(nxk) + є_(nx1). Il modello vuole: analizzare l’influenza che i costi del personale e le altre spese amministrative hanno sulle commissioni attive di un campione di 5 banche; testare l’ipotesi di linearità e verificare la significatività statistica dei regressori. Per testare l’ipotesi di linearità si prende in considerazione la statistica-test F di Fisher la quale presenta un valore del p-value (probabilità della F empirica ovvero il livello minimo di significatività al quale è possibile rifiutare l’ipotesi nulla o di interesse H₀). Dall’output del modello si può dedurre che la statistca-test F di Fisher non è statisticamente significativa al livello di significatività del 5% ( per un test bilatero o a due code 0,05/2=0,025<0,0657). Anche il metodo del confronto fra i valori critici ed empirici della F di Fisher confermano lo stesso risultato per cui si accetta l’ipotesi di non linearità

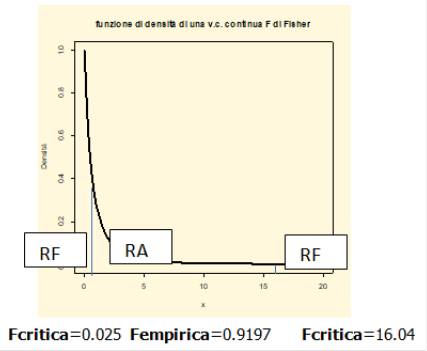
Dal grafico si evince chiaramente che la F empirica cade nella regione di accettazione per cui si accetta che l’ipotesi di linearità non è statisticamente significativa. Le linee di codice per ottenere i valori della F critica sono:

qf(0.025,2,2); qf((1-0.025),2,2). Le line di codice per implementare il modello sono le seguenti:

y<-c((10, 11, 13, 15, 9)

x1<-c(0.4,0.39,0.45,0.65,0.28)

x2<-c(0.11,0.12,0.15,0.09,0.08)

modello<-lm(y~x1+x2);

summary(modello)

Per diagnosticare eventuale presenza di multicollinearità si utilizzano i seguenti strumenti: il coefficiente di determinazione semplice R²; il coefficiente di tolleranza t= 1- R²; il VIF (Variance Inflation Factor)=1/(1- R²); la matrice di correlazione fra le covariate. Il primo è pari a 0.9344 e il secondo t=1-0.9344=0,0656. Entrambi mettono in guardia il ricercatore sulla possibile presenza di multicollinearità tra le covariate. Il terzo è pari VIF=1/(1-R²)=1/0,0656=15,24 che conferma la prenza di multicollinearità nel modello per cui gli stimatoti OLS non sono più efficienti e consistenti. Per quanto riguarda il VIF e la matrice di correlazione si implementano le seguenti linee di codice di R e si ottiene:

library(faraway)

y<-c((10, 11, 13, 15, 9)

x1<-c(0.4,0.39,0.45,0.65,0.28)

x2<-c(0.11,0.12,0.15,0.09,0.08)

modello<-lm(y~x1+x2)

summary(modello)

vif(modello)

Il risultato del vif si riporta di seguito:

x1 x2

1.001132 1.001132

Si ricorda che la scala di misurazione per R è la seguente: per valori >1 c’è un rischio concreto di multicollinearità; per valori >10 massiccia presenza di multicollinarità. Poiché il modello presenta valori, seppur di poco, >1 c’è un rischio concreto di multicollinearità.

x <- matrix (data =c(0.4,0.39,0.45,0.65,0.28, 0.11,0.12,0.15,0.09,0.08), nrow = 5, ncol = 2)

cor(x)

[,1] [,2]

[1,] 1.00000000 0.03362147

[2,] 0.03362147 1.00000000

dove il valore 1 esprime la correlazione fra una covariata e se stessa (x1,x1) e (x2,x2) per i=j mentre 0.03362147 la correlazione fra una e l’altra per i≠j; la scala di misurazione consigliata per i valori di VIF=1/1-R²=15,2439 è la seguente: superiori a 20 forte presenza; tra 7 e 20 rischio di presenza in crescita a partire da 15; inferiori a 7 sostanziale assenza. Nel caso del modello il valore del VIF calcolato indica il rischio concreto di presenza di multicollinearità. Si può dedurre che la scala di misurazione manuale e con R individua il valore 15 corrispondente al valore 1. L’analisi della matrice di correlazione individua un coefficiente pari a 0,033 che di per sé non è molto elevato. Per tentare di risolvere eventuali problemi di multicollinearità si può cercare di far divenire la matrice X a rango pieno aumentando il numero di osservazioni; oppure rimuovere le covariate correlate ed utilizzare le tecniche della principal component regression o ridge regression.

punto c) Per verificare se la covariata aggiunta x3 contribuisce in modo significativo ad aumentare il potere esplicativo del modello1 occorre analizzare il relativo output di R da cui si evince che:

la bontà dell’adattamento ai dati osservati aumenta in quanto l’R²aumenta da 0.934 a 0.9581;

per contro il p-value della statistica-test F di Fisher è meno significativo ovvero viene ancora meno l’ipotesi di linearità;

per quanto riguarda la significatività statistica dei regressori la situazione in questo modello peggiora in quanto, mentre nel primo la covariata era significativa al 5% per un test unilatero destro o del maggiore, tutti i regressori sono non significativi.

punto d) Per verificare se la covariata eliminata x2 contribuisce in modo significativo ad aumentare il potere esplicativo del modello2 occorre analizzare il relativo output di R da cui si evince che:

la bontà dell’adattamento ai dati osservati diminuisce in quanto l’R²passa da 0.934 a 0.903;

per contro il p-value della statistica-test F di Fisher è più significativo del modello 1 ma superiore al modello;

per quanto riguarda la significatività statistica dei regressori la situazione in questo modello migliora rispetto al modello 1 ma peggiora rispetto al modello.

Domanda aperta 3. Prendendo in considerazione i dati del primo modello della domanda aperta 2 presentare: punto a) l’equazione in forma analitica e compatta; punto b) la matrice di varianze inversa di varianze/covarianze; punto c) le varianze dei due coefficienti di regressione e la covarianza; punto a) le varianze dei due coefficienti di regressione e la covarianza in presenza di multicollinearità:

SOLUZIONE: punto a) l’equazione analitica in formula è:

y₁ = β₀+ β₁ x₁₁ + β₂ x₂₁+ є₁

y₂ = β₀+ β₁ x₁₂ + β₂ x₂₂+ є₂

y₃ = β₀+ β₁ x₁₃ + β₂ x₂₃+ є₃

y₄ = β₀+ β₁ x₁₄ + β₂ x₂₄+ є₄

y₅ = β₀+ β₁ x₁₅ + β₂ x₂₅+ є₅

sostituendo con i valori osservati diventa:

10 = 1+ β₁ 0.4 + β₂ 0.11+ є₁

11 = 1+ β₁ 0.39 + β₂ 0.12+ є₂

13 = 1+ β₁ 0.45 + β₂ 0.15+ є₃

15 = 1+ β₁ 0.65 + β₂ 0.09+ є₄

9 = 1+ β₁ 0.28 + β₂ 0.08+ є₅

La matrice X, la sua trasposta X’ e il prodotto XX’ sono riportate di seguito con il calcolo dei singoli valori di varianza e covarianze utilizzando le linee di codice di R:

X <- matrix (data =c(1,1,1,1,1,0.4,0.39,0.45,0.65,0.28,0.11,0.12,0.15,0.09,0.08), nrow = 5, ncol = 3);X

[,1] [,2] [,3]

[1,] 1 0.40 0.11

[2,] 1 0.39 0.12

[3,] 1 0.45 0.15

[4,] 1 0.65 0.09

[5,] 1 0.28 0.08

D<-t(X);D ##matrice trasposta

[,1] [,2] [,3] [,4] [,5]

[1,] 1.00 1.00 1.00 1.00 1.00

[2,] 0.40 0.39 0.45 0.65 0.28

[3,] 0.11 0.12 0.15 0.09 0.08

C<-D%*%X;C ## prodotto XX’

[,1] [,2] [,3]

[1,] 5.00 2.1700 0.5500

[2,] 2.17 1.0155 0.2392

[3,] 0.55 0.2392 0.0635

1^2+1^2+1^2+1^2+1^2 ## varianza x^2(1,1)

[1] 5

0.4^2+0.39^2+0.45^2+0.65^2+0.28^2 ## varianza x^2(2,2)

[1] 1.0155

0.11^2+0.12^2+0.15^2+0.09^2+0.08^2 ## varianza x^2(3,3)

[1] 0.0635

1*0.4+1*0.39+1*0.45+1*0.65+1*0.28 ## covarianza x1*x2(1,2)e covarianza x1*x2(2,1)

[1] 2.17

1*0.11+1*0.12+1*0.15+1*0.09+1*0.08 ## covarianza x1*x3(1,3)e covarianza x1*x2(3,1)

[1] 0.55

0.4*0.11+0.39*0.12+0.45*0.15+0.65*0.09+0.28*0.08 ## covarianza x2*x3(1,3)e covarianza x2*x3(3,1)

[1] 0.2392

Per calcolare la matrice varianze/covarianze inversa (XX’)^-1 e il controllo che moltiplicando XX’ *(XX’)^-1 si ottiene la matrice identità utilizzando le linee di codice di R si ottiene:

N<-solve (C);N ## matrice inversa

[,1] [,2]

[1,] 8.737398 -32.91316

[2,] -32.913159 139.72957

round(C%*%N) ## controllo che il risultato restituisca la matrice identità

[,1] [,2]

[1,] 1 0

[2,] 0 1

Per calcolare le varianze di β1 e β2 e la covarianza /β1, β2) si procede come segue utilizzando le linee di codice di R si procede come segue:

La formula generica per il calcolo della varianza di β1 è: σ² *(∑x_2i)² /(∑x_1i)² * (∑x_2i)²- (∑x_1i x_2i)² sostituendo i valori si ottiene:

(0.11^2+0.12^2+0.15^2+0.09^2+0.08^2) ## numeratore

[1] 0.0635

(0.4^2+0.39^2+0.45^2+0.65^2+0.28^2)*(0.11^2+0.12^2+0.15^2+0.09^2+0.08^2)-((0.4*0.11+0.39*0.12+0.45*0.15+0.65*0.09+0.28*0.08)^2) ## denominatore

[1] 0.00726761

## varianza(β1)=numeratore/denominatore=0.0635/0.00726761=8.737398

La formula generica per il calcolo della varianza di β2 è: σ² *(∑x_1i)² /(∑x_1i)² * (∑x_2i)²- (∑x_1i x_2i)² sostituendo i valori si ottiene:

(0.4^2+0.39^2+0.45^2+0.65^2+0.28^2) ## numeratore

[1] > (0.4^2+0.39^2+0.45^2+0.65^2+0.28^2) ## numeratore

[1] 1.0155

(0.4^2+0.39^2+0.45^2+0.65^2+0.28^2)*(0.11^2+0.12^2+0.15^2+0.09^2+0.08^2)-((0.4*0.11+0.39*0.12+0.45*0.15+0.65*0.09+0.28*0.08)^2) ## denominatore

[1] 0.00726761

## varianza(β2)=numeratore/denominatore=1.0155/0.00726761=139.72957

la formula generica per il calcolo della covarianza di β1, β2 è: -σ² *(∑x_1i x_2i /(∑x_1i)² * (∑x_2i)²- (∑x_1i x_2i)² sostituendo i valori si ottiene:

-(0.4*0.11+0.39*0.12+0.45*0.15+0.65*0.09+0.28*0.08) ## numeratore

[1] -0.2392

(0.4^2+0.39^2+0.45^2+0.65^2+0.28^2)*(0.11^2+0.12^2+0.15^2+0.09^2+0.08^2)-((0.4*0.11+0.39*0.12+0.45*0.15+0.65*0.09+0.28*0.08)^2) ## denominatore

[1] 0.00726761

## covarianza(β1,β2)=numeratore/denominatore= -0.2392/0.00726761= -32.91316

In presenza di multicollinearità ipotizzando che x1 sia legata da una relazione lineare con x2 secondo la formula= x_1i=αx_1i+x_2i quindi ∑x_1i x_2i=α∑x²_1i; sostituendo si ottiene:

La formula generica per il calcolo della varianza di β1 diventa: σ² *(∑x_2i)² /(∑x_1i)² * (∑x_2i)²-α ∑x_1i²

La formula generica per il calcolo della varianza di β2 diventa: σ² *(∑x_1i)² /(∑x_1i)² * (∑x_2i)²- α ∑x_2i²

La formula generica per il calcolo della covarianza di β1, β2 diventa: -σ² * α ∑x_2i² /(∑x_1i)² * (∑x_2i)²- α ∑x_2i²

E’ facile intuire che maggiore è il valore di α maggiore è la relazione lineare tra le due covariate: poiché il termine al denominatore α ∑x_2i² ha il segno meno all’aumentare dello stesso, per effetto dell’aumento di α, diminuisce l’intero denominatore aumentando di conseguenza la varianza e rendendo inutilizzabili gli stimatori OLS che non sono i più efficienti.

Domanda aperta 4. Si estragga dal CRAN di R il data set iris e, utilizzando i codici di R, si voglia: punto a) spiegare la differenza fra modello additivo e con iterazione; punto b) svolgere una diagnostica attraverso l’analisi grafica; punto c) presentare l’ANOVA dei due modelli; punto d) presentare il grafico dei valori assoluti dei residui standardizzati dei due modelli.

SOLUZIONE: punto a) nella specificazione di un modello di regressione lineare multipla, oltre al problema dell’individuazione corretta delle variabili di interesse, si può decidere di implementare lo stesso in due modi: il primo, facendo agire le covariate separatamente oppure congiuntamente verificando come cambia l’influenza sulla variabile dipendente; nel caso del data set iris se le covariate Petal.Length + Petal.Width agiscono separatamente il modello si definisce additivo; se agiscono congiuntamente il modello si definisce con iterazione e le linee di codice di R sono le seguenti:

data(iris)

modello <- lm(Sepal.Length ~ Petal.Length + Petal.Width, data = iris)

summary(modello)

modello_con iterazione <- lm(Sepal.Length ~ Petal.Length*Petal.Width, data = iris)

summary(modello1)

L’output del modello additivo è:

Call:

lm(formula = Sepal.Length ~ Petal.Length + Petal.Width, data = iris)

Residuals:

Min 1Q Median 3Q Max

-1.18534 -0.29838 -0.02763 0.28925 1.02320

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 4.19058 0.09705 43.181 < 2e-16 ***

Petal.Length 0.54178 0.06928 7.820 9.41e-13 ***

Petal.Width -0.31955 0.16045 -1.992 0.0483 *

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.4031 on 147 degrees of freedom

Multiple R-squared: 0.7663, Adjusted R-squared: 0.7631

F-statistic: 241 on 2 and 147 DF, p-value: < 2.2e-16

//////////////////////////////////////////////////////////////////////////////////////////////////////

L’output del modello con iterazione è:

Call:

lm(formula = Sepal.Length ~ Petal.Length * Petal.Width, data = iris)

Residuals:

Min 1Q Median 3Q Max

-1.00058 -0.25209 0.00766 0.21640 0.89542

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 4.57717 0.11195 40.885 < 2e-16 ***

Petal.Length 0.44168 0.06551 6.742 3.38e-10 ***

Petal.Width -1.23932 0.21937 -5.649 8.16e-08 ***

Petal.Length:Petal.Width 0.18859 0.03357 5.617 9.50e-08 ***

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’

Residual standard error: 0.3667 on 146 degrees of freedom

Multiple R-squared: 0.8078, Adjusted R-squared: 0.8039

F-statistic: 204.5 on 3 and 146 DF, p-value: < 2.2e-16

Analizzando I due output si evince chiaramente che il modello con iterazione presenta una maggiore bontà di adattamento ai dati e una più alta significatività statistica dei regressori.

punto b) per svolgere una diagnostica attraverso l’analisi grafica si implementano i seguenti codici di R:

par(mfcol = c(2,4))

par(bg="cornsilk")

plot(modello,main="modello additivo")

plot(modello, main="modello con interazione")

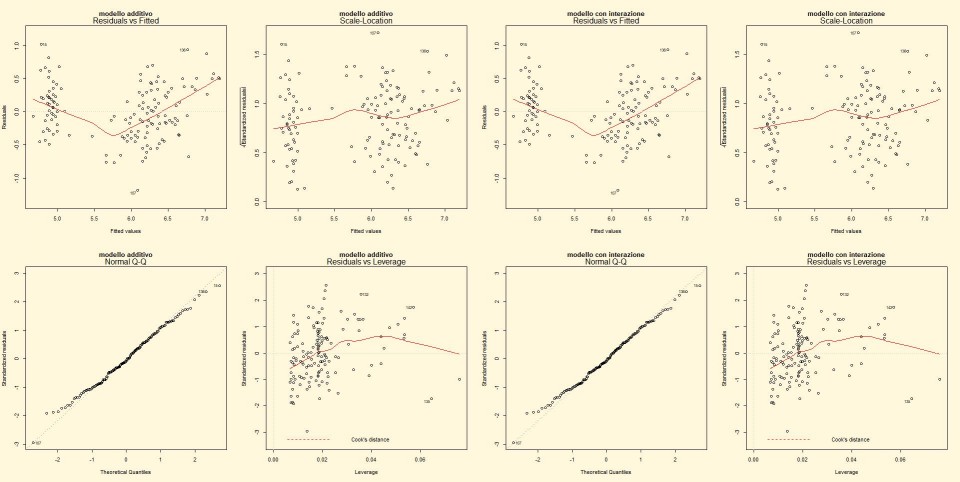
punto c) Per presentare l’ANOVA dei due modelli la linea di codice di R è:

anova(modello,modello1)

L’output che R resituisce è:

Analysis of Variance Table

Model 1: Sepal.Length ~ Petal.Length + Petal.Width

Model 2: Sepal.Length ~ Petal.Length * Petal.Width

Res.Df RSS Df Sum of Sq F Pr(>F)

1 147 23.881

2 146 19.637 1 4.2441 31.556 9.502e-08 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Dai dati dell’ANOVA si evince che anche la devianza residua degli errori stimati (RSS) è più bassa nel modello con iterazione rispetto a quello additivo.

punto d) Si implementano i seguenti codici di R per l’analisi grafica dei valori dei residui studentizzati:

par(mfcol = c(1,2))

par(bg="cornsilk")

qqPlot(modello, main="QQ Plot – modello additivo")

qqPlot(modello1, main="QQ Plot – modello con interazione")

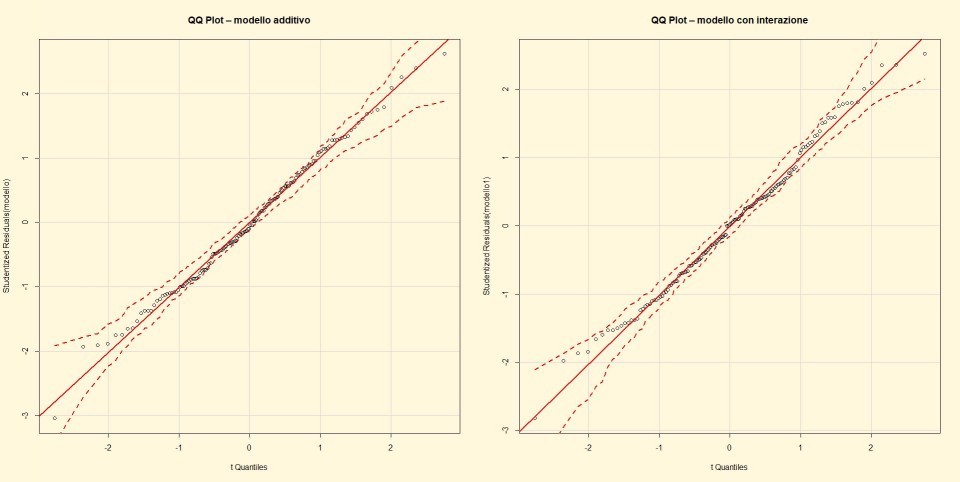
Osservando attentamente il grafico si può notare che l’intervallo dei residui studentizzati è leggermente più stretto nel modello con iterazione rispetto a quello additivo

Domanda aperta 5. Dati i seguenti valori di y (121,110,100,90,80,75,70,64,58,57,56,55,48,44,42) e di x<-c(1.9,2.4,2.5,2.6,2.7,2.8,2.9,3.3,3.8,4.3,4.5 implementare: punto a) il modello polinomiale; punto b) il modello log-lineare e lineare-log; punto c) il modello log-log; punto a) effettuare il confronto fra i 4 modelli e scegliere il migliore svolgendo un sintetico commento.

SOLUZIONE: punto a) per implementare il modello 1 si eseguono le seguenti linee di codice di R:

library(labstatR)

y<-c(121,110,100,90,80,75,70,64,58,57,56,55,48,44,42)

x<-c(1.9,2.4,2.5,2.6,2.7,2.8,2.9,3.3,3.8,4.3,4.5,

4.8,8.1,8.8,9.1)

z<- x^2

modello1 <- lm(y ~ x+z)

summary(modello1)

L’output che si ottiene è il seguente:

Call:

lm(formula = y ~ x + z)

Residuals:

Min 1Q Median 3Q Max

-12.9929 -7.5890 -0.7167 7.2338 13.8221

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 181.1805 15.8473 11.433 8.28e-08 ***

x -42.9055 7.0062 -6.124 5.15e-05 ***

z 3.1199 0.6175 5.053 0.000283 ***

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 9.291 on 12 degrees of freedom

Multiple R-squared: 0.8754, Adjusted R-squared: 0.8546

F-statistic: 42.15 on 2 and 12 DF, p-value: 3.742e-06

punto b) per implementare i modello 2 e 3 si eseguono le seguenti linee di codice di R:

library(labstatR)

y<-c(121,110,100,90,80,75,70,64,58,57,56,55,48,44,42)

x<-c(1.9,2.4,2.5,2.6,2.7,2.8,2.9,3.3,3.8,4.3,4.5,

4.8,8.1,8.8,9.1)

z<-log(y)

modello2<-lm(z~x)

summary(modello2)

w<-log(x)

modello3<-lm(y~w)

summary(modello3)

Gli output che si ottengono sono i seguenti:

Call:

lm(formula = z ~ x)

Residuals:

Min 1Q Median 3Q Max

-0.21373 -0.15864 -0.02051 0.09615 0.29990

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 4.71761 0.09535 49.475 3.44e-16 ***

x -0.11669 0.01949 -5.986 4.55e-05 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.176 on 13 degrees of freedom

Multiple R-squared: 0.7338, Adjusted R-squared: 0.7133

F-statistic: 35.83 on 1 and 13 DF, p-value: 4.547e-05

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

Call:

lm(formula = y ~ w)

Residuals:

Min 1Q Median 3Q Max

-13.358 -9.201 -5.981 9.008 19.920

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 128.661 9.314 13.813 3.80e-09 ***

w -42.970 6.570 -6.541 1.88e-05 ***

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 12.21 on 13 degrees of freedom

Multiple R-squared: 0.7669, Adjusted R-squared: 0.749

F-statistic: 42.78 on 1 and 13 DF, p-value: 1.881e-05

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

punto c) per implementare il modello 4 si eseguono le seguenti linee di codice di R:

y<-c(121,110,100,90,80,75,70,64,58,57,56,55,48,44,42)

x<-c(1.9,2.4,2.5,2.6,2.7,2.8,2.9,3.3,3.8,4.3,4.5,

4.8,8.1,8.8,9.1)

z<-log(y)

w<-log(x)

modello3<-lm(z~w)

summary(modello3)

L’output che si ottiene è il seguente:

Call:

lm(formula = z ~ w)

Residuals:

Min 1Q Median 3Q Max

-0.1548 -0.0910 -0.0438 0.1042 0.2021

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 5.03773 0.09526 52.882 < 2e-16 ***

w -0.61606 0.06719 -9.169 4.88e-07 ***

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1249 on 13 degrees of freedom

Multiple R-squared: 0.8661, Adjusted R-squared: 0.8558

F-statistic: 84.06 on 1 and 13 DF, p-value: 4.878e-07

punto d) il modello migliore dal punto di vista della bontà di adattamento ai dati è quello polinomiale che presenta un valore del coefficiente di determinazione pari a 0.8754 mentre dal punto di vista della statistica-test F di Fisher il migliore è il modello log-log che presenta un valore del quantile della F empirica pari a 42.78 con un p-value pari 4.878e-07

##################################################################

Appunti per lezioni del 29 e 30 Aprile 2019

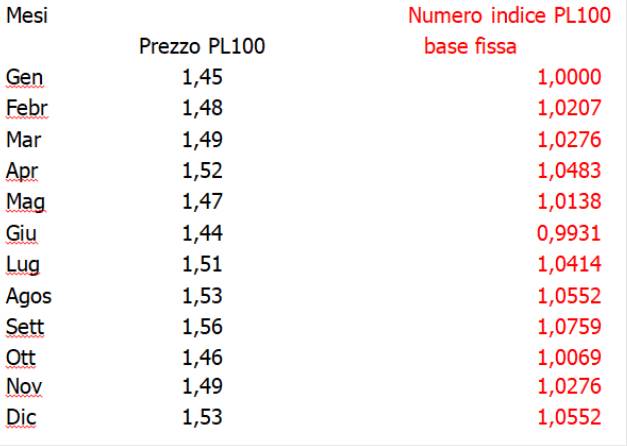
Numeri indice a base fissa

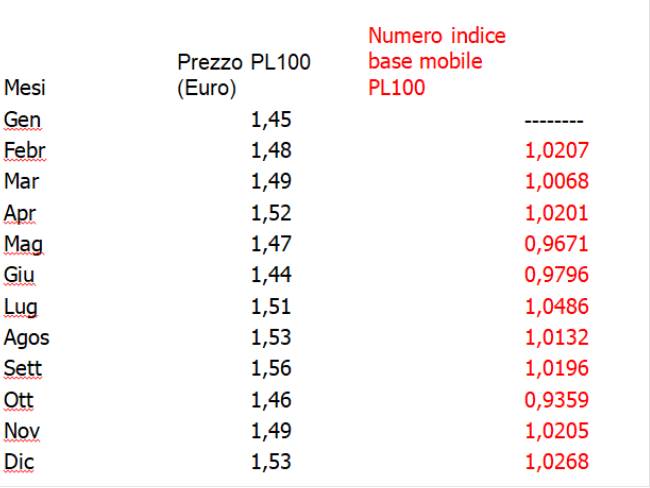
Per calcolare i numeri indice a base fissa si applica la seguente notazione: ₀I₁= x₁/x₀

Nel caso riportato sotto la notazione, per base Gennaio, diventa:

Gennaio ₀I₁=(1,45/1,45)*100=100,00; Febbraio ₀I₂=(1,48/1,45)*100=102,07 e così di seguito. Si può dedurre che il numero indice di Febbraio, a base Gennaio, del prezzo del prodotto PL100 ha subito una variazione positiva del 2,07%

Data la seguente notazione:

₀I₁= (x₁ - x₀) / x₀ = x₁/x₀ -1=₀I₁-1

Si perviene allo stesso risultato applicandola al mese di Febbraio:

₀I₂= (x₂ - x₀) / x₀ = x₂/x₀ -1=₀I₂-1=1,0207-1=0,027*100=2,07%

Numeri indice a base mobile

Per calcolare i numeri indice a base mobile si applica la seguente notazione:

_t-1I_t= x_t/x_t-1

In questo caso il calcolo parte dal Febbraio non disponendo del prezzo del mese di Dicembre dell’anno precedente:

Febbraio _febI_genn=(1,48/1,45)*100=102,07. Si può constatare che il numero indice a base mobile di Febbraio coincide con quello a base fissa e quindi il prezzo del prodotto PL100 ha subito una variazione positiva del 2,07%

Dal mese di Marzo in poi i due indici differiscono.

Infatti quello di Marzo sarà dato da:

Febbraio _marzoI_febbr=(1,49/1,48)*100=100,68

Si può dedurre che mentre il numero indice a base fissa del Mese di Marzo è pari 102,76 con un incremento dello 0,69% quello a base mobile restituisce un valore pari a 100,68 con un decremento pari a 1,39% per cui è evidente l’effetto prezzo che si muove da un mese all’altro mentre l’indice a base fissa è rapportato sempre allo stesso prezzo detto appunto prezzo base

Numero indice complesso di Laspeyres

Dati i seguenti valori dei prezzi e delle quantità del prodotto PL100:

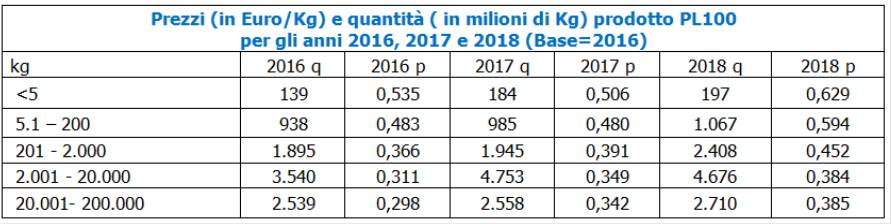
Si redige la tabella propedeutica per il calcolo dei numeri indici di Laspeyres, Paasche e Fisher

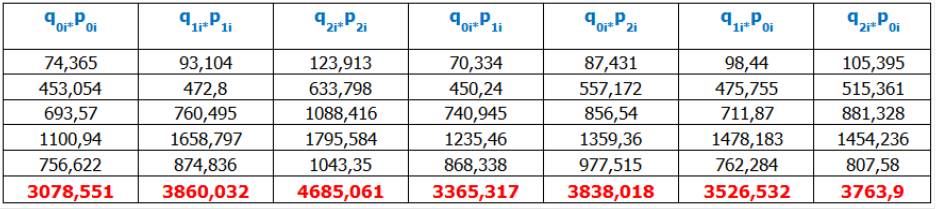
La notazione per il calcolo del numero indice di Laspeyres è la seguente:

I _Laspeyres=∑_i(p_{it *}q_i0)/ ∑_i(p_{i0 *}q_i0)

La notazione per il calcolo del numero indice di Paasche è la seguente:

I_Paasche=∑_i(p_{it *}q_it)/ ∑_i(p_{i0 *}q_it)

La notazione per il calcolo del numero indice di Fisher è la seguente:

I_Fisher=Rdq(I_Paasche* I _Laspeyres)

Di seguito si riportano i calcoli di controllo:

Medie mobili a termini dispari

Si riportano di seguito i valori dei prezzi del prodotto PL100 del primo semestre degli anni 2015, 2016, 2017 e 2018. Essi possono essere considerati come una serie storica mensile relativa ad un determinato periodo.

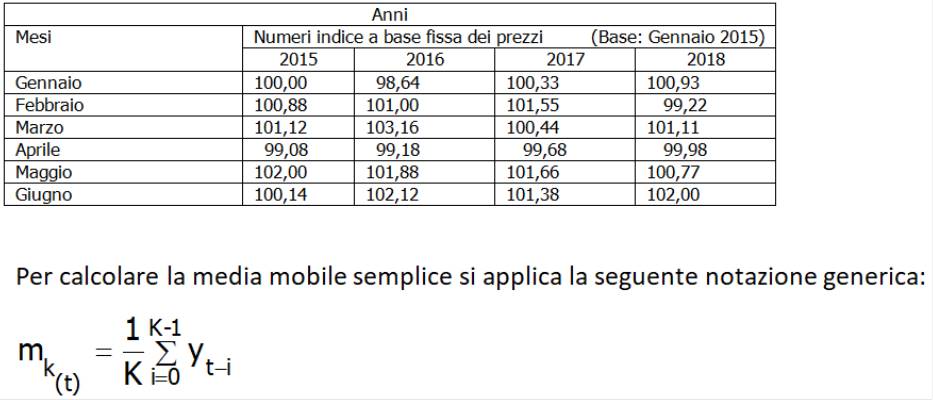
Si applichi ai dati di cui sopra stabilendo che la media mobile semplice sia di ordine k=3 e che t=3

M₃₁=1/3∑^3-1_i=0 y_t-i=(y₃+ y₃ +y₂ )/3=(99,8+101,12+100,88)/3=301,8/3=100,6

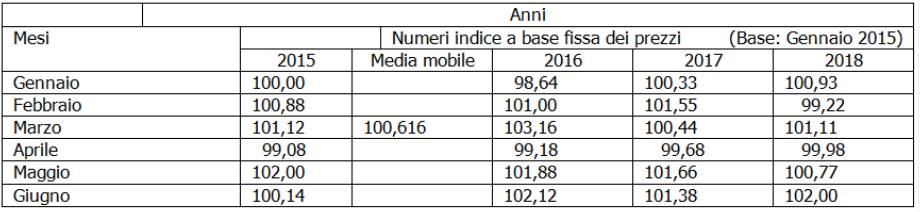
Si può notare che si perdono i primi e gli ultimi due termini. Se invece la media mobile per K=3 è centrata se ne perdono solo 1.

Medie mobili a termini pari

La media mobile centrata per K pari è data dalla notazione:

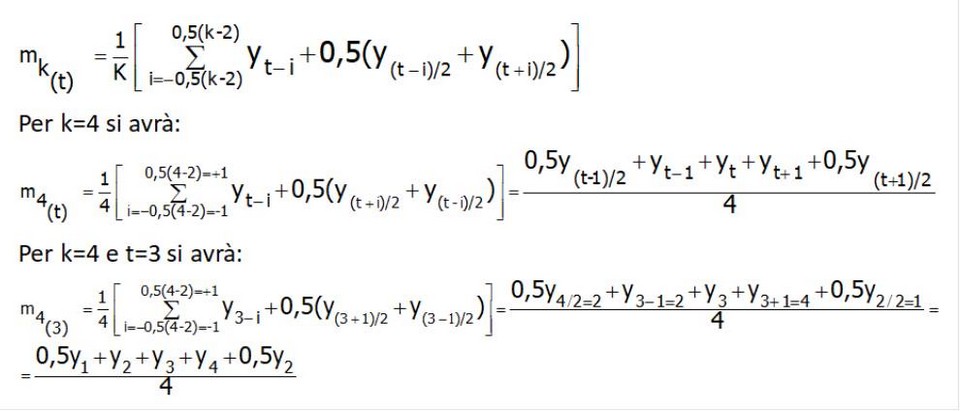
Si può constatare che la media mobile centrata per k pari è configurabile come una media mobile ponderata nella quale il peso del primo e dell’ultimo termine è la metà del peso di tutti gli altri. Per serie storiche mensili con K=12 la media mobile ponderata diventa:

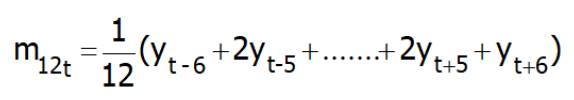
Si riporta di seguito la tabella con i dati dei tassi armonizzati sui prestiti per acquisto abitazioni e della quantità di prestiti concessi alle famiglie residenti di un Gruppo bancario

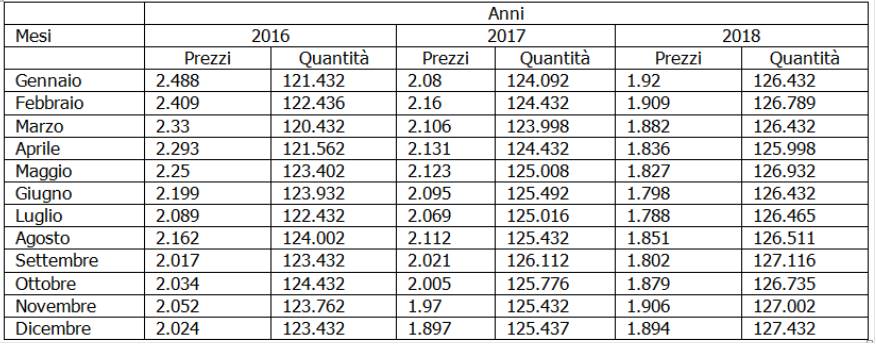
Per calcolare il numero indice complesso di Laspeyres per i tre anni (Anno Base=2016) si applica la seguente notazione:

I _{Laspeyres 2016}=∑_i(p_{t *}q₀)/ ∑_i(p_{0 *}q₀)

Per calcolare il numero indice complesso di Paasche per i tre anni (Anno Base=2016) si applica la seguente notazione:

I_Paasche=∑_i(p_{it *}q_it)/ ∑_i(p_{i0 *}q_it)

Per calcolare il numero indice complesso di Fisher per i tre anni (Anno Base=2016) si applica la seguente notazione:

I_Fisher=Rdq(I_Paasche* I _Laspeyres)

Modelli Holt-Winters

I tre parametri di smussamento esponenziale dei modelli Holt-Winters sono tre: alfa, beta e gamma, rispettivamente utilizzati per il livello, il trend e la stagionalità della serie storica.

##################################################################

Appunti sui Processi stocastici 7e 8 Maggio 2019

Processi stocastici

Un processo stocastico { Y_t } _t_ϵ_T può essere definito come una famiglia di v.c. in sequenza y₁ , y₂,……, y_t indicizzate in uno spazio campionario discreto Ω=T con T=t₁, t₁,……., t_n , legate ad una legge di probabilità congiunta fra le stesse v.c. e definite in uno spazio di probabilità (Ω, D, P). Si ricorda che Ω rappresenta lo spazio degli eventi elementari di cui è composto lo spazio campionario, D il dominio che, come detto sopra, può essere discreto o continuo e P che è la probabilità del verificarsi degli eventi elementari. Se T=[0,∞) le v.c. sono indicizzate in uno spazio campionario continuo. Per T = {1}), il processo { Y_t } _t_ϵ_T è rappresentato da una sola v.c.. Quando T assume valori finiti (ad es. T = {1, 2, ..., n}) si ottiene un vettore di v.c.. Un processo stocastico modella l’evoluzione di un sistema casuale nel tempo che, come detto sopra, può essere discreto o continuo. Sostanzialmente si può dire che esso simula una serie storica. Il concetto di simulazione è molto importante per costruire un sistema casuale nel tempo. Alla base della simulazione c’è la generazione dei numeri casuali secondo una determinata legge probabilistica. Se si estrae una sequenza indipendente di valori da una distribuzione di probabilità di una v.c. uniforme discreta da 0 a1 oppure di una v.c. normale standardizzata si ottengono i numeri casuali.

Per quanto riguarda i momenti di un processo stocastico si rimanda al libro di testo Par.16.2 pg.238.

Script per ottenere numeri casuali da distribuzioni discrete e continue

Esempio 1. Estrazione di 20 numeri casuali dalla distribuzione di probabilità della v.c. discreta binomiale con n=22 e p=0,7 (spazio di probabilità (Ω, D, P) (22,25,0.7)

## CODICE DI R ##

x <- 0:25

n <- 22

p <- 0.7

rbinom(20,size=22,prob=0.25)

par(bg="cornsilk")

plot(rbinom(20,22,0.25), xlab="prove",ylab="numeri casuali estratti",main=” Grafico dei numeri casuali estratti”, type="h",lwd=5)

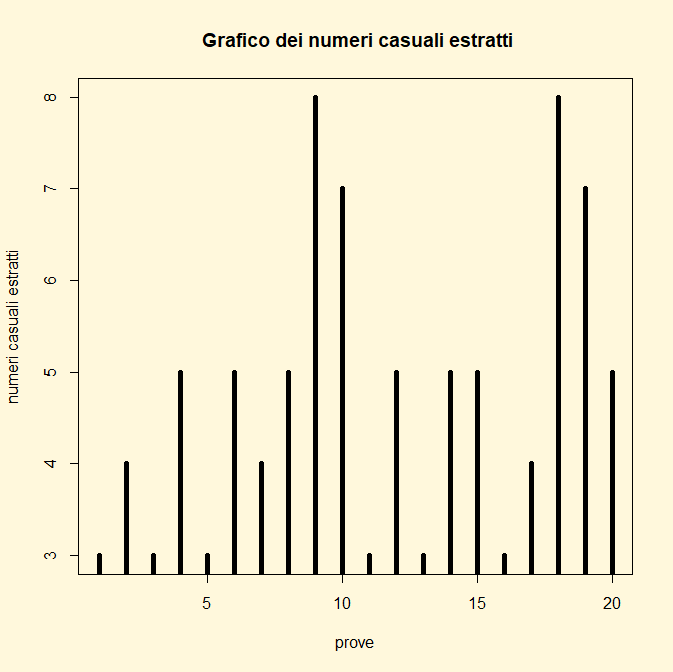
Se i numeri casuali estratti dalla legge binomiale si volessero rappresentare sotto forma di serie storica si dovrebbero implementare le seguenti linee di codice di R.

## CODICE DI R ##

library(tseries)

yt<-c(8,4,3,6,6,4,6,6,5,6,7,6,5,5,2,3,5,4,5)

par(bg="cornsilk")

ts.plot(yt, xlab="prove",ylab="numeri casuali estratti", main="Simulazione serie storica da Binomiale", lwd=5)

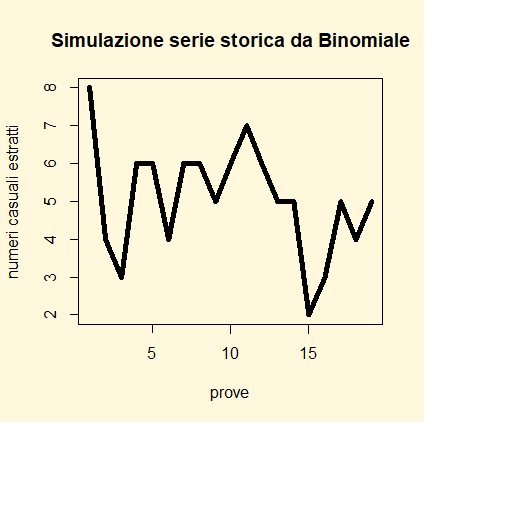
Processo stocastico “white noise”

Si ribadisce che con il software R si simulano le realizzazioni di una serie di processi stocastici dai più semplici ai più complessi.

Si inizia con il più elementare ovvero con un processo stocastico “white noise”. In primo luogo si definisce “white noise” il processo stocastico {є_t} costituito da una serie di v.c. incorrelate a media 0 e varianza costante.

Esso si distribuisce secondo la seguente notazione:

w_t ~ WN(0,σ²) con E(w_t)=0; E(w_t²)= σ²

La funzione di autocovarianza si può esprimere secondo la seguente notazione:

Autocov(w_t w_s) =0 per ogni t≠s

Se w_t rappresenta una v.c distribuita secondo una normale il processo stocastico si definisce “white noise gaussiano”.

Poiché il processo è, come detto sopra, costituito da v.c incorrelate, se queste sono normali si può affermare che sono anche indipendenti.

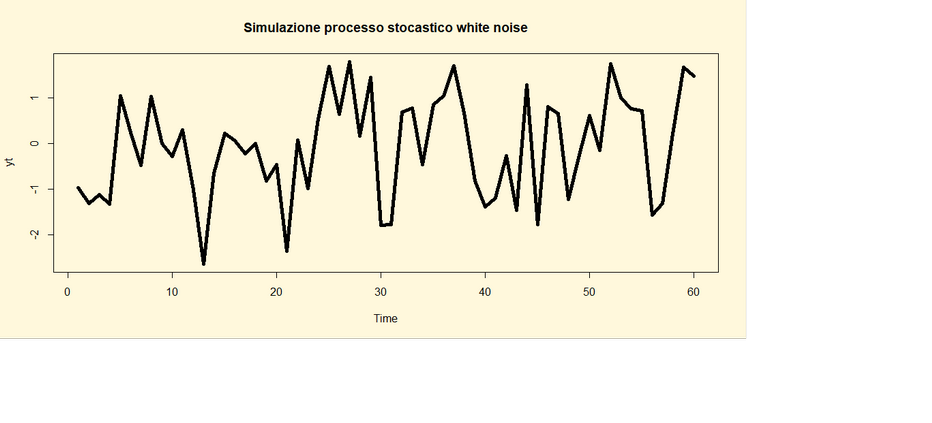
Le linee di codice per implementare tale processo sono:

## CODICE DI R ##

library(tseries)

yt<-arima.sim(list(order=c(0,0,0)),n=180)

par(bg="cornsilk")

ts.plot(yt, xlab="tempo",ylab="valori del processo", main="Simulazione processo stocastico white noise" ,lwd=5)

Va fatto presente che gli argomenti del comando arima.sim sono order che sta ad indicare l’ordine del processo ARIMA(p,d,q); in questo processo p=d=q=0 in linea con le premesse teoriche sopra specificate ed n che indica il numero di valori simulati. Il comando ts.plot serve per implementare il grafico del processo che viene rappresentato sotto.

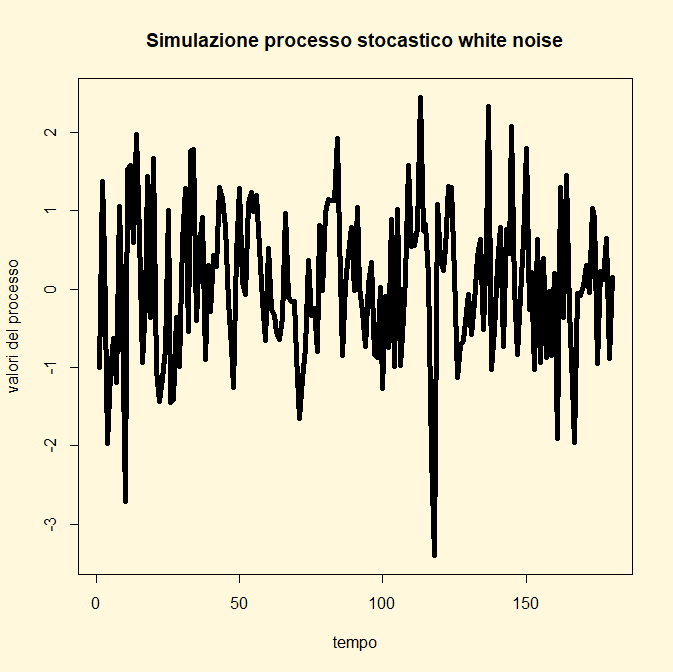
Come si può osservare i valori simulati oscillano più o meno regolarmente intorno ad E(є_t)=0 e il loro livello sopra e sotto lo 0 è allo stesso tempo più o meno regolare confermando la tesi teorica che la varianza è costante V(є_t)= σ²

Per poter capire meglio il comportamento del processo si implementano le funzioni di autocorrelazione totale (ACF) e parziale (PACF). Le linee di codice di R per implementarli sono le seguenti:

## CODICE DI R ##

library(tseries)

yt<-arima.sim(list(order=c(0,0,0)),n=180)

par(mfrow=c(2,1))

par(bg="cornsilk")

acf(yt, lag.max=20,, main="Grafico ACF campionaria(h=0,1,….,20)" ,lwd=5)

pacf(yt, lag.max=20="tempo",ylab="valori del processo", main="Grafico ACF campionaria(h=0,1,….,20)" ,lwd=5)

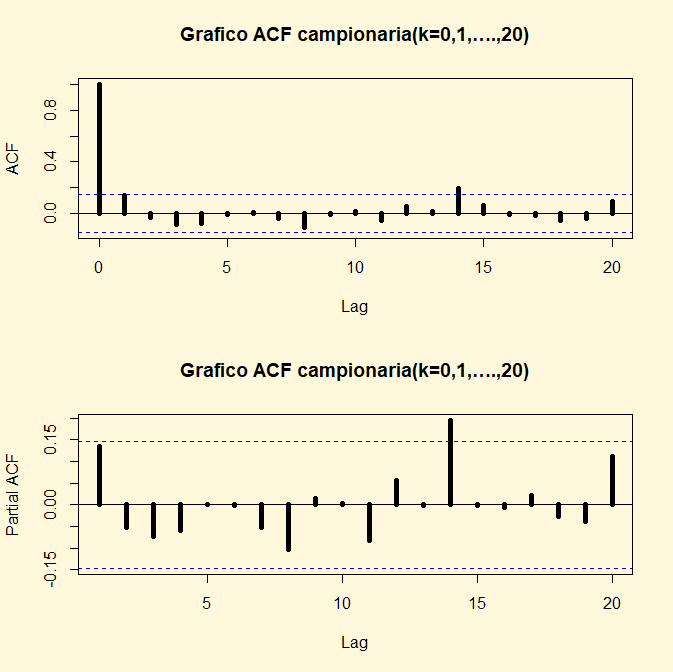
Occorre precisare gli argomenti che sono collegati alla funzione ACF; innanzitutto il processo stocastico che simula la serie (nel caso in questione {y_t} composto da 180 realizzazioni o valori simulati; quindi i valori di r (rapporto di autocorrelazione riportati sull’asse delle ordinate ed ottenuti applicando la formula della funzione di autocorrelazione stessa data da:

r=ρ(k)/ ρ(0) =∑_t=1^n-k(y_t+k-y_nmedia) *(y_t-y_nmedia)/ ∑_t=1^n-k(y_t-y_nmedia)²

L’altro argomento è lag.max=20 che sta ad indicare il numero dei ritardi k pari a 20 sui quali si intende calcolare r. Da qui si capisce che quando k=0 r è sempre uguale a 1 (r=ρ(0)/ ρ(0) =1).

Lo stesso vale per la PACF.

Nell’analisi dei due correlogrammi si può notare che sono tratteggiate due riche parallele all’asse delle ascisse che stanno ad indicare gli estremi superiore ed inferiore dello stimatore intervallare. Dato il seguente sistema di ipotesi:

H₀: ρ(0)=0 vs H₁: ρ(0)≠0

e stabilito il livello di significatività (ad esempio al 5%) si può stabilire se accettare o rifiutare l’ipotesi nulla o di interesse.

Applicando il teorema del limite centrale e quindi per n abbastanza grande (>30) il rapporto r si distribuisce asintoticamente secondo una normale ρ(k)~N(0,1/RDQ(n).

A questo punto applichiamo le notazioni al processo stocastico {y_t}; la prima è relativa ad r che diventa per k=1,2:

r=ρ(1)/ ρ(0) =∑_t=1^180-1(y₁₈₀₊₂₀-y₁₈₀media) *(y₁₈₀-y₁₈₀media)/ ∑_t=1^180-1(y₁₈₀-y₁₈₀media)²

r=ρ(2)/ ρ(0) =∑_t=1^180-2(y₁₈₀₊₂₀-y₁₈₀media) *(y₁₈₀-y₁₈₀media)/ ∑_t=1^180-2(y₁₈₀-y₁₈₀media)²

e così via fino a k=20

Per quanto riguarda la regola di decisione la notazione diventa:

Ad un livello di significatività del 5% la z_α/2 critica per un test bilatero è pari a±1,96 e quindi il dominio è

| ρ(k)|>1,96/ RDQ(n).

quindi per n=180 il limite superiore è pari a 1,96/ RDQ(180)=1,96/13,4164=0,146 mentre il limite inferiore è pari a

-1,96/ RDQ(180)=1,96/13,4164=-0,146

Osservando la funzione di autocorrelazione parziale si può notare che al ritardo 14 il valore di r è esterno all’intervallo dello stimatore intervallare per cui si è propensi a rifiutare l’ipotesi nulla o di interesse H₀.

Da quanto esposto sopra si può dedurreche il processo white noise w_t modella quello che nella modellistica econometrica è il termine di errore.

Processo stocastico autoregressivo “AR(p)”

Innanzitutto va specificato il significato del parametro p. Esso sta a significare il grado del polinomio del processo. La notazione generica con cui lo si esprime è la seguente:

Y_t=φ₀+ φ₁ Y_t_-1+………+ φ_p Y_t_-p+ є_t

In questa sede si esamina solo il caso del processo AR(1) che assume di conseguenza la seguente notazione:

Y_t=φ₀+ φ₁ Y_t_-1+ є_t

dove φ₀ e φ₁ sono i due coefficienti dei valori della serie ritardata di un periodo ed є_t un processo white noise є_t ~ WN(0,σ²)

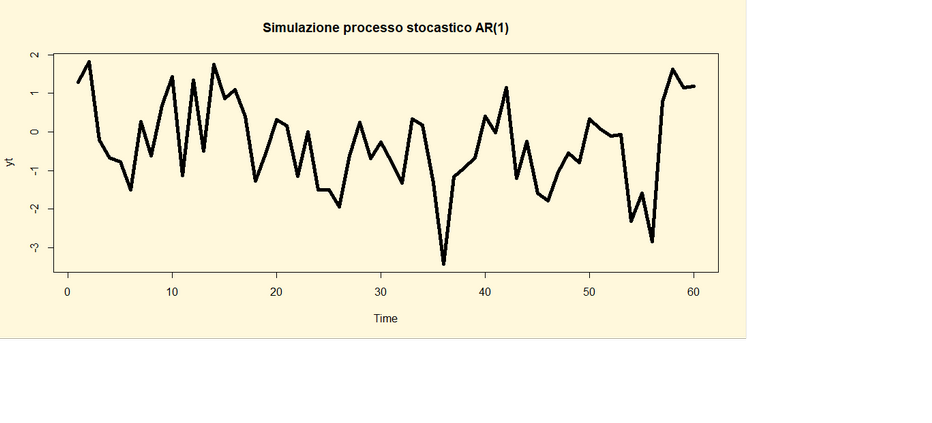
Esempio. Si simuli un processo stocastico AR(1) con n=180 e φ₁=0.19, privo di φ₀. La notazione che lo esprime è la seguente:

Y_t=0,19 Y_t_-1+ є_t

e lo si voglia rappresentare graficamente.

Le linee di codice di R che si implementano sono le seguenti:

## CODICE DI R ##

library(tseries)

yt<-arima.sim(list(order=c(1,0,0),ar=0.19),n=180)

par(bg="cornsilk")

ts.plot(yt, type="l", main="Simulazione processo stocastico AR(1)" ,lwd=5)

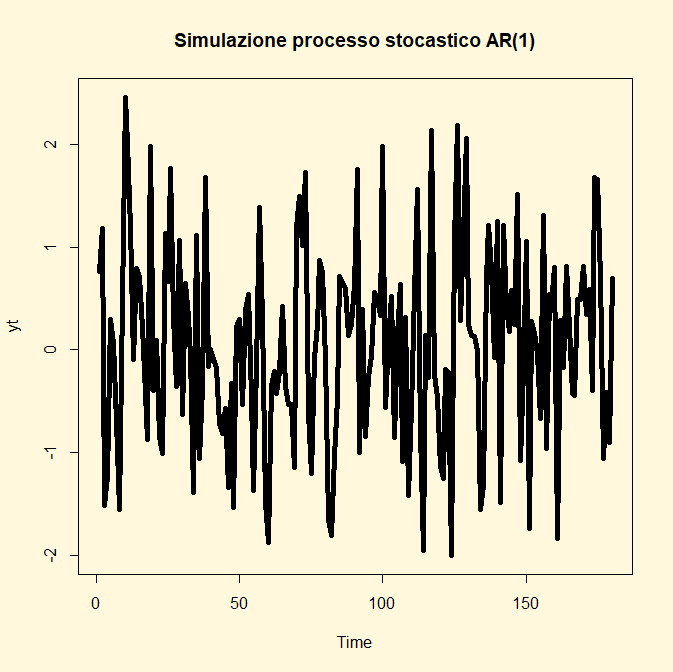
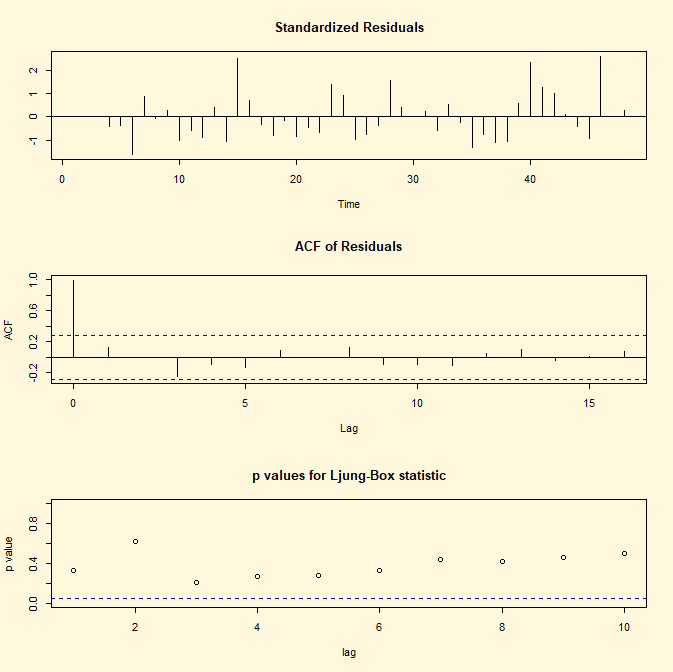
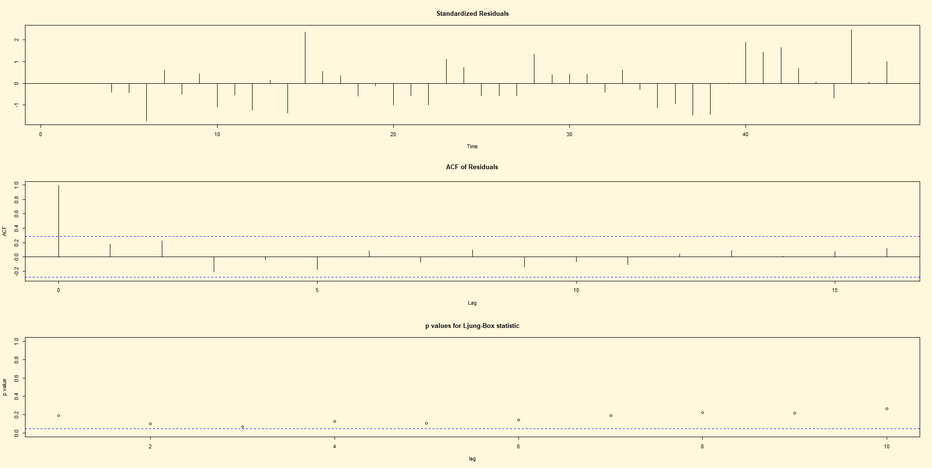
Per svolgere il procedimento inverso ovvero stimare i coefficienti φ₀ e φ₁ di un processo stocastico AR(1) e rappresentare il grafico, l’ACF e il test Ljung-Box si implementano le seguenti linee di codice di R:

## CODICE DI R ##

library(tseries)

fit <- arima(lh, c(1,0,0)) ;fit

par(bg="cornsilk")

tsdiag(fit)

## RISULTATO ##

Call:

arima(x = lh, order = c(1, 0, 0))

Coefficients:

ar1 intercept

0.5739 2.4133

s.e. 0.1161 0.1466

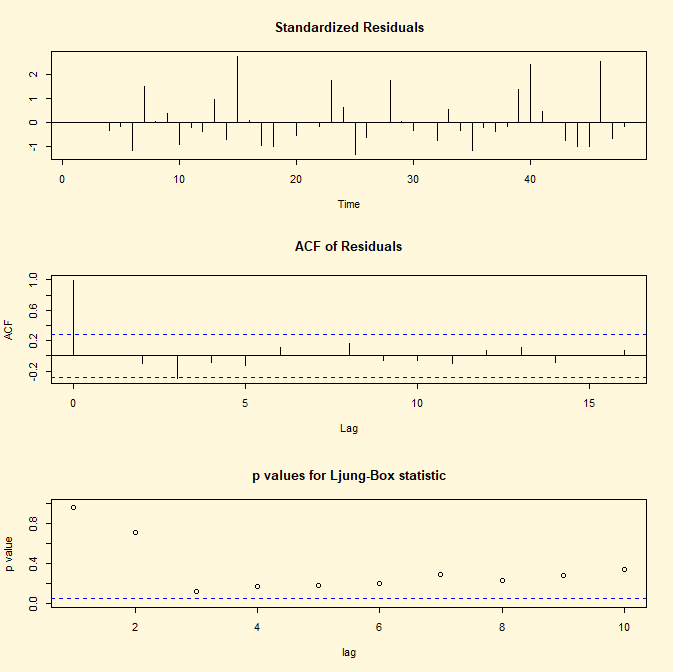
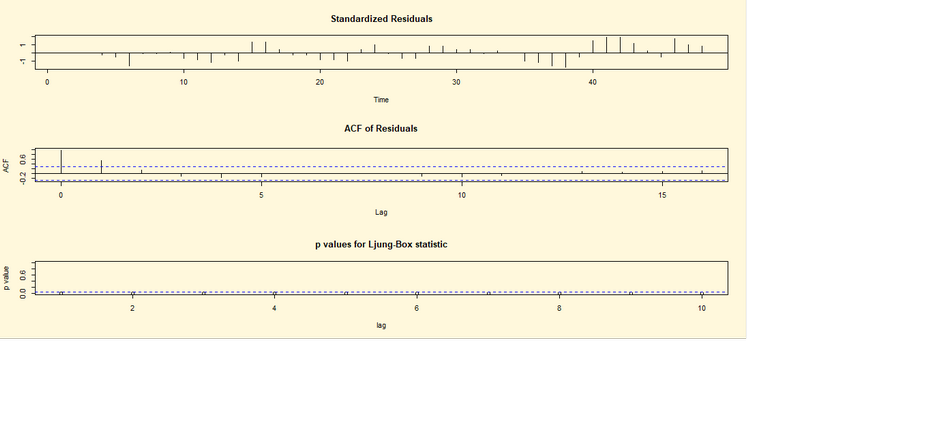
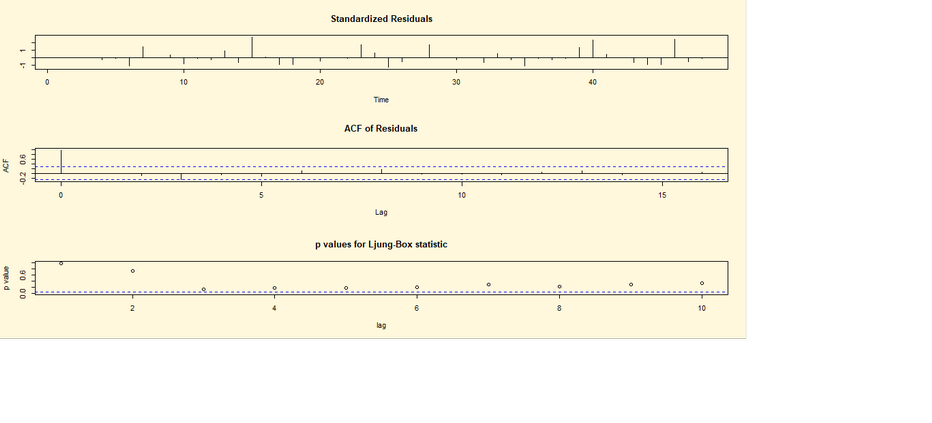
Per svolgere il procedimento inverso ovvero stimare solo il coefficienti φ₁ di un processo stocastico AR(1) e rappresentare il grafico, l’ACF e il test Ljung-Box (p-value in funzione dei ritardi) si implementano le seguenti linee di codice di R:

## CODICE DI R ##

library(tseries)

fit <- arima(lh, c(1,1,0)) ;fit

par(bg="cornsilk")

tsdiag(fit)

## RISULTATO ##

Call:

arima(x = lh, order = c(1, 1, 0))

Coefficients:

ar1

-0.0404

s.e. 0.1443

sigma^2 estimated as 0.2525: log likelihood = -34.35, aic = 72.7

Processo stocastico a media mobile“MA(q)”

Innanzitutto va specificato il significato del parametro q. Esso sta a significare il grado del polinomio del processo. La notazione generica con cui lo si esprime è la seguente:

Y_t= є_t-θ₁+ є_t-1 - ……….+ θ_q є_t-q

In questa sede si esamina solo il caso del processo MA(1) che assume di conseguenza la seguente notazione:

Y_t= є_t+ θ₁є_t-1

dove θ₁ è il coefficiente dei valori della serie ritardata di un periodo ed є_t un processo white noise є_t ~ WN(0,σ²)

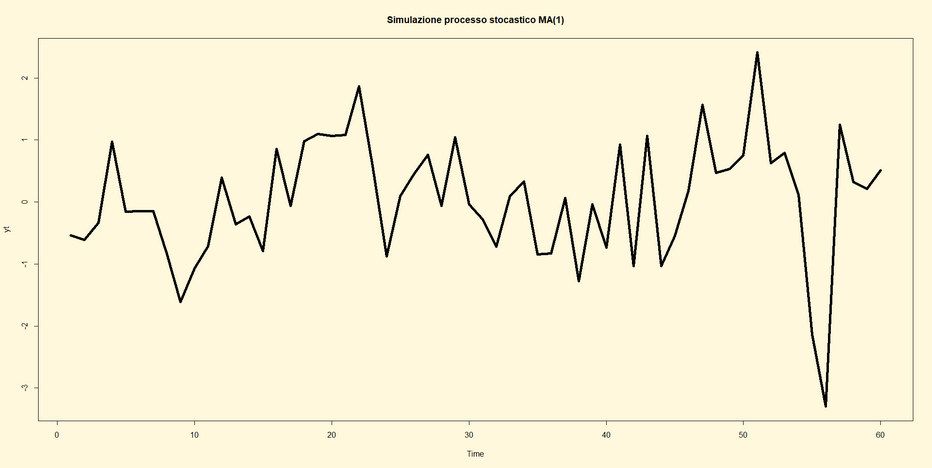
Esempio 1. Si simuli un processo stocastico MA(1) con n=180 e θ₁=0.48. La notazione che lo esprime è la seguente:

Y_t= є_t+ 0,48є_t-1

e lo si voglia rappresentare graficamente.

Le linee di codice di R che si implementano sono le seguenti:

## CODICE DI R ##

library(tseries)

yt<-arima.sim(list(order=c(0,0,1),ar=0.48),n=180)

par(bg="cornsilk")

ts.plot(yt, type="l", main="Simulazione processo stocastico MA(1)" ,lwd=5)

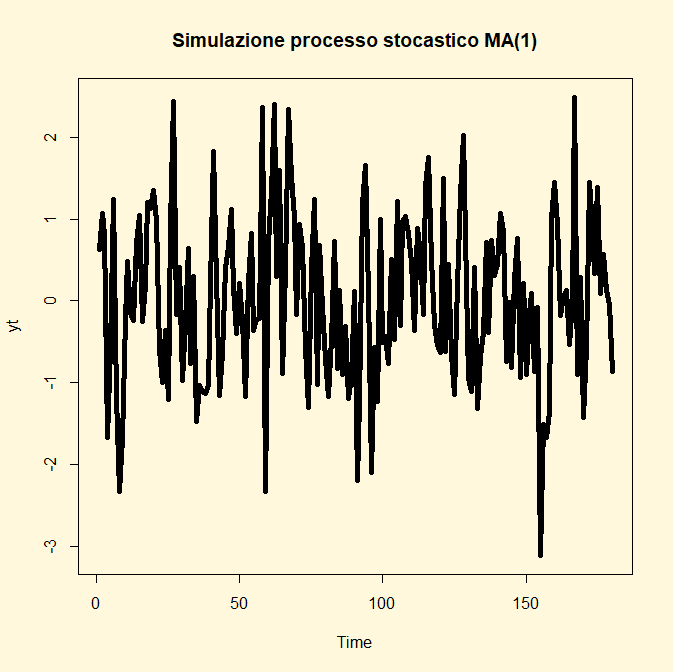
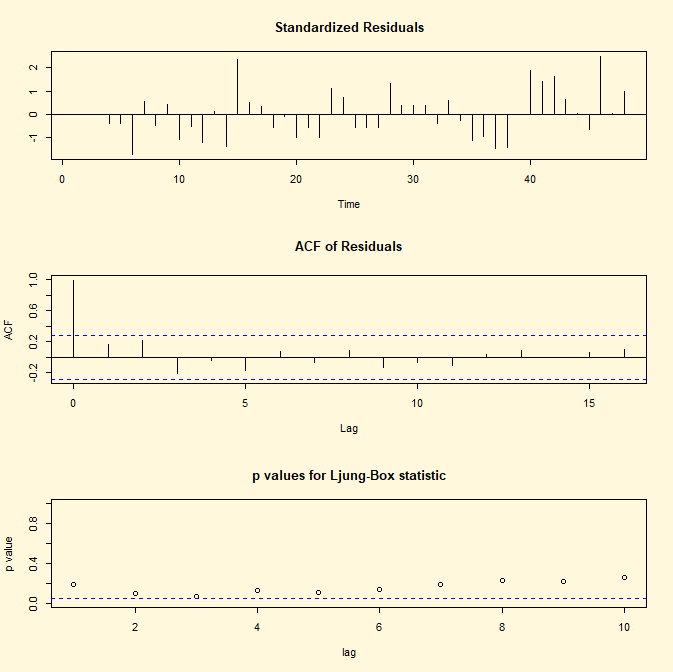
Per svolgere il procedimento inverso ovvero stimare il coefficienti θ₁di un processo stocastico MA(1) con intercetta e rappresentare il grafico, l’ACF e il test Ljung-Box (p-value in funzione dei ritardi) si implementano le seguenti linee di codice di R:

## CODICE DI R ##

library(tseries)

fit <- arima(lh, c(0,0,1)) ;fit

par(bg="cornsilk")

tsdiag(fit)

## RISULTATO ##

Call:

arima(x = lh, order = c(0, 0, 1))

Coefficients:

ma1 intercept

0.4810 2.4051

s.e. 0.0944 0.0979

sigma^2 estimated as 0.2123: log likelihood = -31.05, aic = 68.1

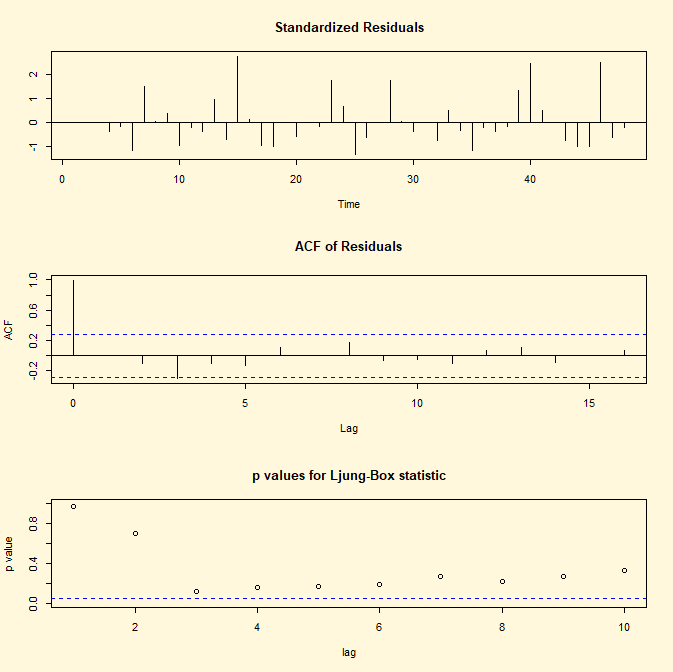
Per svolgere il procedimento inverso ovvero stimare il coefficienti θ₁di un processo stocastico MA(1) senza intercetta e rappresentare il grafico, l’ACF e il test Ljung-Box (p-value in funzione dei ritardi) si implementano le seguenti linee di codice di R:

## CODICE DI R ##

library(tseries)

fit <- arima(lh, c(0,1,1)) ;fit

par(bg="cornsilk")

tsdiag(fit)

## RISULTATO ##

Call:

arima(x = lh, order = c(0, 1, 1))

Coefficients:

ma1

-0.0533

s.e. 0.1712

sigma^2 estimated as 0.2524: log likelihood = -34.34, aic = 72.68

Stazionarietà di un processo stocastico

Si parla di processo stocastico stazionario in due sensi: stazionarietà forte (anche detta in senso stretto) e stazionarietà debole. Per definire la stazionarietà forte, prendiamo in esame un sottoinsieme delle variabili casuali che compongono il processo; queste non devono necessariamente essere consecutive, ma per aiutare l’intuizione, facciamo finta che lo siano. Consideriamo perciò una ‘finestra’ aperta sul processo di ampiezza k, ossia un sottoinsieme del tipo W^k_t = (x_t, . . . , x_t+k−1)

Questa è naturalmente una variabile casuale a k dimensioni, con una sua funzione di densità che, in generale, può dipendere da t. Se però ciò non accade, allora la distribuzione di W^k_t è uguale a quella di W^k_t+1,W^k_t+2 e così via. Siamo in presenza di stazionarietà forte quando questa invarianza vale per qualsiasi k. In altri termini, quando un processo è stazionario in senso forte le caratteristiche distribuzionali di tutte le marginali rimangono costanti al passare del tempo.

La stazionarietà debole, invece, riguarda solo finestre di ampiezza 2: si ha stazionarietà debole se tutte le variabili casuali doppie W²_t = (x_t, x_t+1), hanno momenti primi e secondi costanti nel tempo; da questo discende che esistono anche tutti i momenti secondi incrociati E(xt· xt+k), con k qualunque, e anch’essi non dipendono da t (anche se possono dipendere da k). È per questo motivo che la stazionarietà debole viene anche definita stazionarietà in covarianza…”.

########################################################

Appunti per lezioni 14 e 15 Maggio 2019

Processi stocastici ARMA(p,q)

La notazione generica con cui si esprime un processo stocastico ARMA(p,q) è la seguente:

Y_t=φ₀+ φ₁ Y_t_-1+………+ φ_p Y_t_-p+ є_t + θ₁є_t-1 +……….+ θ_q є_t-q

Si può facilmente constatare che il processo è composto, come stabilito dalla teoria, dalla componente autoregressiva e a media mobile. In questa sede si analizza soltanto il processo ARMA(1,1) la cui notazione è:

Y_t=φ₀+ φ₁ Y_t-₁+ є_t + θ₁є₁

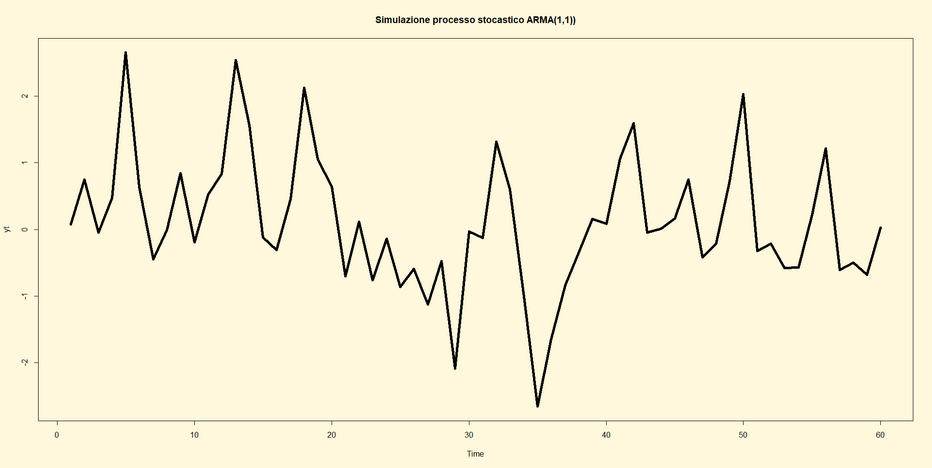
Dato il seguente processo stocastico (privo di intercetta):

Y_t=0,45 Y_t-₁+ є_t + 0,5 є₁

Le linee di codice per implementarlo e rappresentarlo graficamente sono le seguenti:

##Codice di R ##

library(tseries)

yt <- arima.sim(list(order=c(1,0,1), ar=0.45, ma=0.5), n=210)

par(bg="cornsilk")

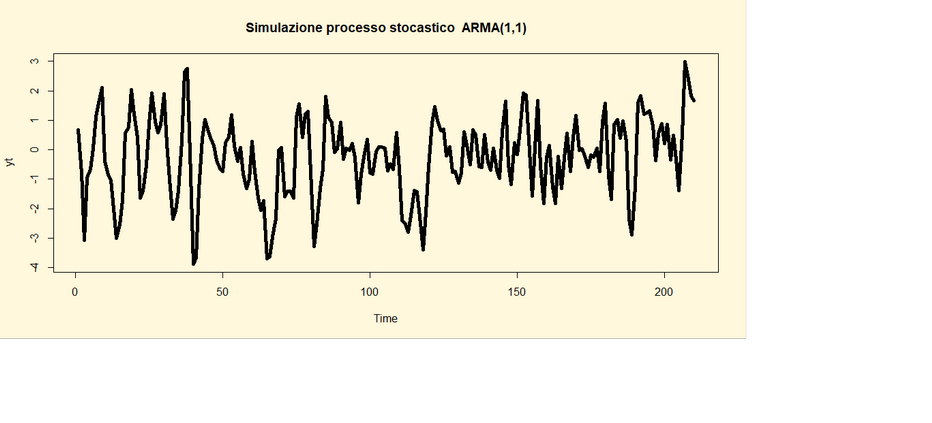
ts.plot(yt, type="l", main="Simulazione processo stocastico ARMA(1,1)" ,lwd=5)

Per implementare esattamente la funzione di autocorrelazione di un qualsiasi processo ARMA il comando di R da usare `e ARMAacf(). Prendendo a riferimento lo stesso processo stocastico sopra descritto ed un numero di ritardi max pari a 10le linee di codice di R sono le seguenti:

##Codice di R ##

library(tseries)

rho <- ARMAacf(ar=0.45, ma=c(0.5), lag.max=10);rho

par(bg="cornsilk")

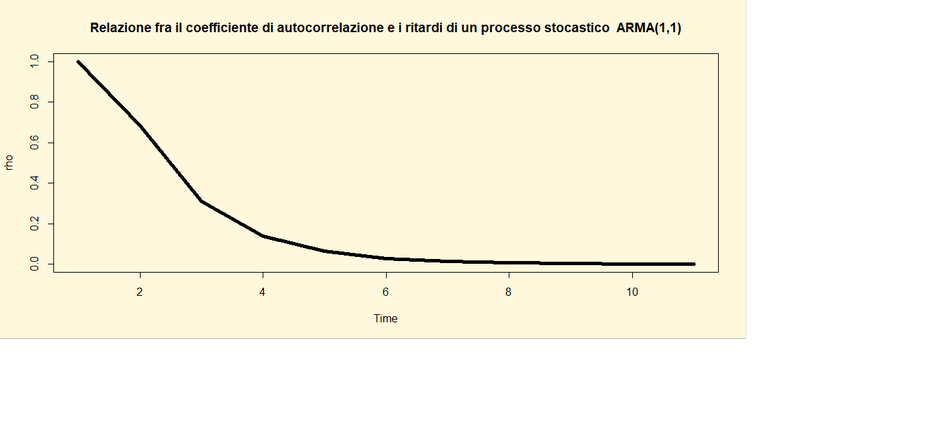
ts.plot(rho, type="l", main="Relazione fra il coefficiente di autocorrelazione e i ritardi di un processo stocastico ARMA(1,1)" ,lwd=5)

##Risultato ##

0 1 2 3 4 5

1.0000000000 0.6845588235 0.3080514706 0.1386231618 0.0623804228 0.0280711903

6 7 8 9 10

0.0126320356 0.0056844160 0.0025579872 0.0011510942 0.0005179924

Gli argomenti che sono inseriti nel comando ARMAacf sono i seguenti:

• ar=c(..,..,..) rappresenta i valori numerici dei coefficienti delle componenti autoregressive, se presenti. Qualora si intenda calcolare la funzione di autocorrelazione di un processo MA (senza componenti AR) `e sufficiente porre ar=0

• ma=c(..,..,..) rappresenta i valori numerici dei coefficienti delle componenti a media mobile, sesenti. Come in precedenza, se non sono presenti componenti MA, occorre inviare ma=0

• lag.max ovvero il numero di ritardi k in corrispondenza dei quali si intende far calcolare la funzione di autocorrelazione.

Con il comando ts.plot(rho,….) si intende rappresentare graficamente la relazione fra il coefficiente di autocorrelazione e i ritardi di un processo stocastico ARMA(1,1).

Per rappresentare graficamente le funzioni di autocorrelazione totale e parziale del processo stocastico ARMA(1,1) con coefficienti ar=0,45 e ma=0,5 si implementano le seguenti linee di codice di R:

##Codice di R ##

yt<-arima.sim(list(order=c(1,0,1), ar=0.4,5, ma=0.5), n=210)

par(mfrow=c(2,1))

par(bg="cornsilk")

acf(yt)

pacf(yt)

L’esame dei due grafici conferma che la serie si smorza a 0 già al ritardo 7.

Si ritiene utile fare alcune considerazioni sulla struttura della serie. La prima riguarda la presenza di trend e/o stagionalità che contribuisce a rendere non stazionarie le serie storiche effettivamente osservate. In questi casi occorre depurare la serie da tali

componenti in modo da renderle stazionarie e identificare il modello ARMA che meglio si adatti alla nuova serie (stazionaria) di dati. Per la stima del trend si possono usare filtri lineari del tipo “medie mobili” semplici e ponderate e i modelli additivi e moltiplicativi stagionali di Holt-Winters per i quali si rimanda agli argomenti trattati nei precedenti Appunti.

La seconda riguarda la differenziazione della serie storica. E’ notorio che una serie storica può essere detrendizzata (o destagionalizzata) applicando gli operatori differenza espressi dalle seguenti notazioni:

∇^d = (1 − B)^d ∇^D_p= (1 − B^p)^D

dove B è l’operatore ritardo e p la periodicità stagionale.

Per implementare una serie differenziata si utilizza il comando di R diff()

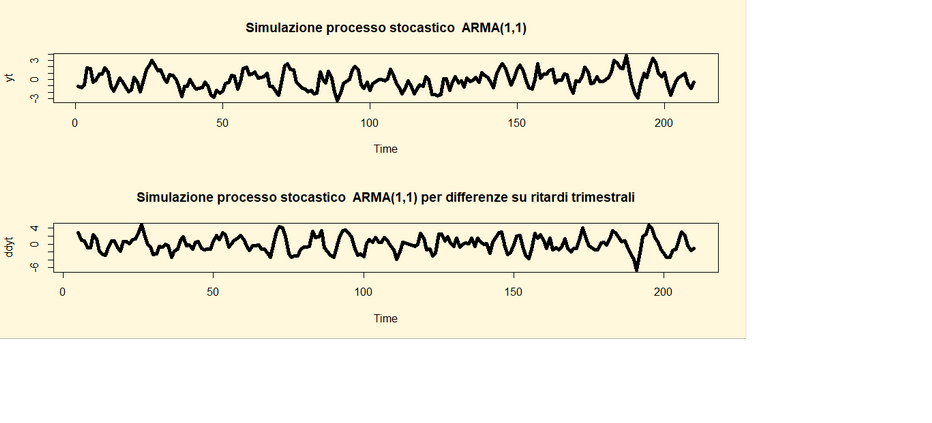
Si riprenda il processo stocastico ARMA(1,1) con coefficienti ar=0,45 e ma=0,5 e lo si implementi attraverso l’operatore ritardo d=1 con ritardi trimestrali applicando le seguenti linee di codice di R:

##Codice di R ##

library(tseries)

yt <- arima.sim(list(order=c(1,0,1), ar=0.45, ma=0.5), n=210)

ddyt <- diff(yt, lag=4, differences=1)

par(mfrow=c(2,1))

par(bg="cornsilk")

plot(yt, main="Simulazione processo stocastico ARMA(1,1)" ,lwd=5)

plot(ddyt, main="Simulazione processo stocastico ARMA(1,1) per differenze su ritardi trimestrali" ,lwd=5)

Processi stocastici ARIMA(p,d,q)

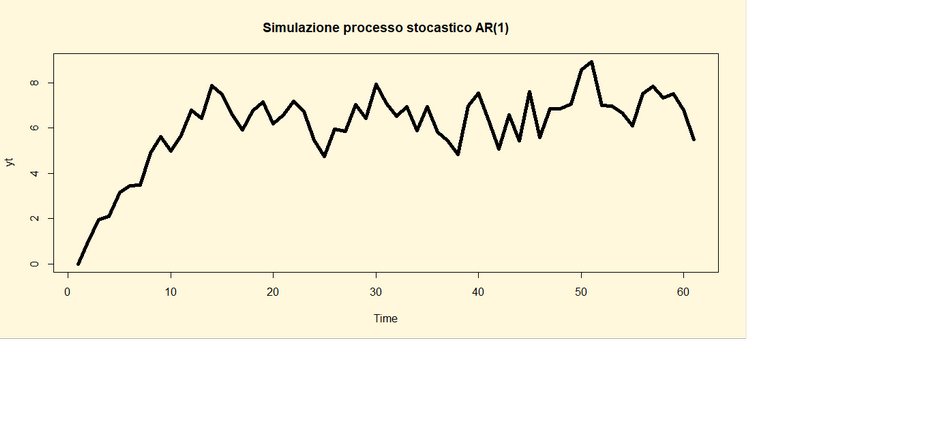
Si riportano di seguito le linee di codice per implementare i modelli ARIMA(p,d,q)

library(tseries)

ar1<-arima.sim(n=100,list(order=c(1,1,0),ar=0.6));ar1

par(bg="cornsilk")

plot(ar1, main="Simulazione di un processo AR(1)")

library(tseries)

ar1<-arima.sim(n=100,list(order=c(1,0,0),ar=0.6));ar1

par(bg="cornsilk")

plot(ar1, main="Simulazione di un processo AR(1)")

library(tseries)

ar11<-arima.sim(n=50, list(ar=0.15, sd=sqrt(2.5)));ar11

par(bg="cornsilk")

plot(ar11, main="Simulazione di un processo AR(1,1)")

library(tseries)

ar2<-arima.sim(n=100, list(order=c(2,1,0), ar=c(0.5,0.4)));ar2

par(bg="cornsilk")

plot(ar2, main="Simulazione di un processo AR(2)")

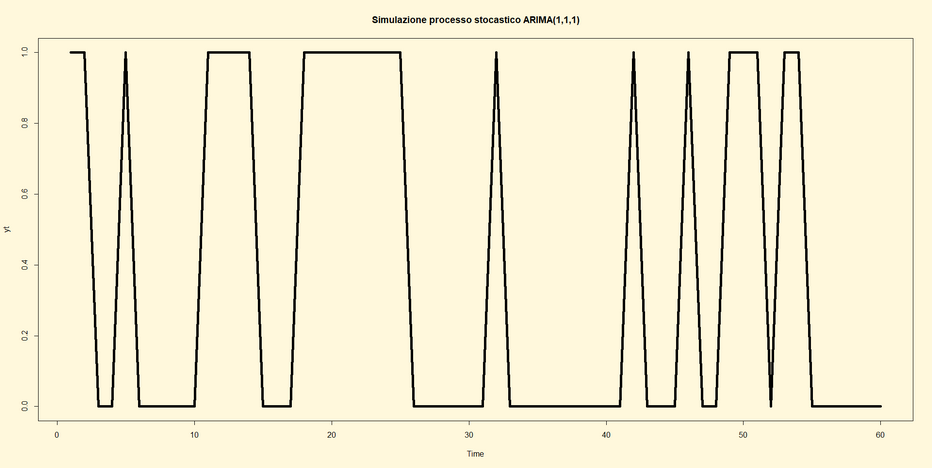
library(tseries)

arima1<-arima.sim(n=50, list(order=c(1,1,1), ar=0.2, ma=-0.3));arima1

par(bg="cornsilk")

plot(arima1, main="Simulazione di un processo ARIMA(1,1,1)")

library(tseries)

arimafit2<-arma(arima1, order=c(1,1), include.intercept=FALSE);arimafit2

summary(arimafit2)

library(tseries)

ar11<-arima.sim(n=50, list(ar=0.9381,ma=-0.29901));ar11

par(bg="cornsilk")

plot(ar11, main="Simulazione di un processo AR(1,1)")

Esercitazione di Macroeconometria.

Si vuole svolgere un’analisi completa sulla serie storica delle variazioni trimestrali del Pil Italia dal 1998 al 2012. Si riporta di seguito lo script che ci aiuta a capire tutti i concetti teorici studiati. Si inizia con le linee di codice di R con le quali si riprendono i dati della serie storica, li si struttura per trimestre e li si rappresenta graficamente.

##Codice di R ##

library(tseries)

VarPil<-c(-0.6024, 0.5596, 0.0911, -0.36, 0.4271, 0.5885, 0.78, 1.3433, 1.0021,

0.9387, 0.5798, 1.2726, 0.6955, -0.4718, -0.3578, -0.112, 0.1745, 0.4069, 0.2465,

0.1215, -0.1463, -0.2668, 0.2397, 0.5372, 0.5384, 0.3165, 0.2641, 0.1471, -0.1526,

0.7718, 0.6666, 0.1601, 0.5681, 0.5458, 0.3631, 1.0501, 0.3811, -0.0337, -0.128,

-0.1706, 0.9143, -0.7503, -1.293,-2.3081, -3.0173, -0.3981, 0.5795, 0.0798, 0.5317,

0.731, 0.5047, 0.3567, 0.3755, 0.1956, -0.527, -1.0241, -1.0052, -0.6155, -0.5349,

-0.5215);VarPil

yt <-ts(VarPil, start=c(1998,1), end=c(2012,4), frequency=4);yt

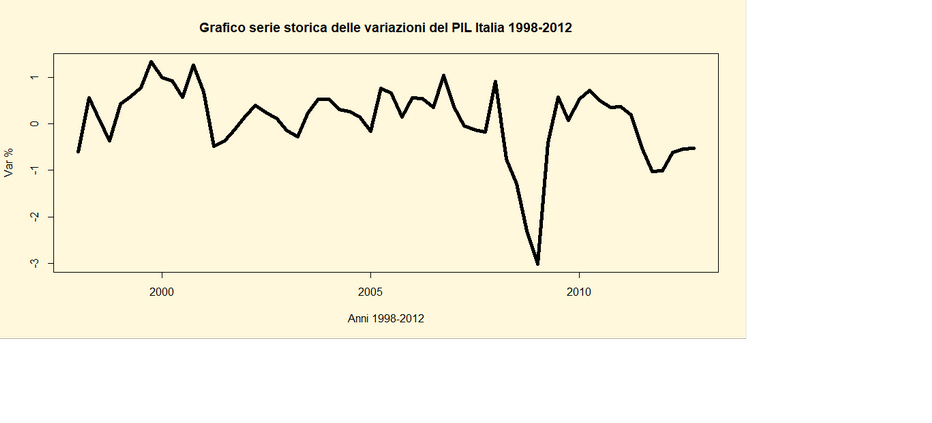
par(bg="cornsilk")

ts.plot(yt, main="Grafico serie storica delle variazioni del PIL Italia 1998-2012",ylab="Var %",

xlab="Anni 1998-2012", lwd=5)

Si riporta il grafico della serie storica.

Si vuole ora svolgere un’analisi descrittiva sulla serie rappresentando anche il box-plot.

##Codice di R ##

summary(yt)

par(bg="cornsilk")

boxplot(yt,main="Box-plot serie storica delle variazioni del PIL Italia 1998-2012")

##Risultato ##

Min. 1st Qu. Median Mean 3rd Qu. Max.

-3.01700 -0.28950 0.24310 0.08749 0.56170 1.34300

Se si volesse aprire una finestra all’interno della serie, ad esempio dal 2007 al 2012 ovvero a partire dalla crisi dei subprime americani si implementano le seguenti linee di codice di R.

##Codice di R ##

yt07<-window(yt, start=c(2007,1), end=c(2012,4));yt07

sum(yt07)

##Risultato ##

Qtr1 Qtr2 Qtr3 Qtr4

2007 0.3811 -0.0337 -0.1280 -0.1706

2008 0.9143 -0.7503 -1.2930 -2.3081

2009 -3.0173 -0.3981 0.5795 0.0798

2010 0.5317 0.7310 0.5047 0.3567

2011 0.3755 0.1956 -0.5270 -1.0241

2012 -1.0052 -0.6155 -0.5349 -0.5215

[1] -7.6774

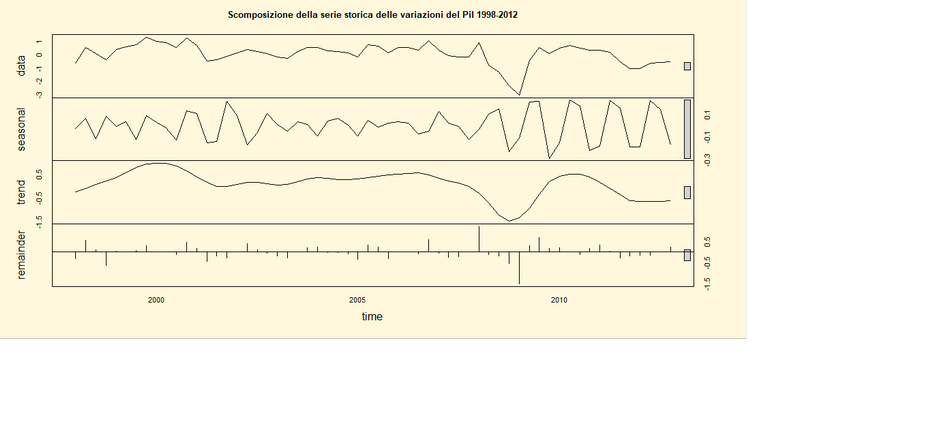
A questo punto si vuole scomporre la serie nelle sue componenti Trend/Ciclo, Stagionale e Casuale e rappresentarle graficamente implementando le seguenti linee di codice di R.

##Codice di R ##

yt1<-stl(yt, s.window=7);yt1

par(bg="cornsilk")

plot(yt1, main="Scomposizione della serie storica delle variazioni del Pil 1998-2012"

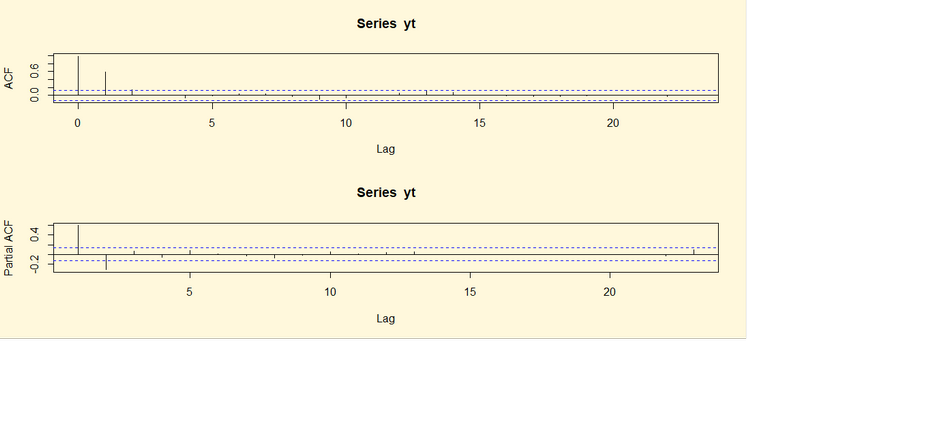
Ora si vuole analizzare la serie attraverso le funzioni di autocorrelazione totale e parziale implementando le seguenti linee di codice di R.

##Codice di R ##

par(mfrow=c(2,1))

par(bg="cornsilk")

acf(yt, main="Funzione di autocorrelazione campionaria totale")

pacf(yt, main="Funzione di autocorrelazione campionaria parziale")

Dall’analisi delle funzioni di autocorrelazione totale e soprattutto parziale emerge che la serie accetta l’ipotesi nulla.

##Codice di R ##

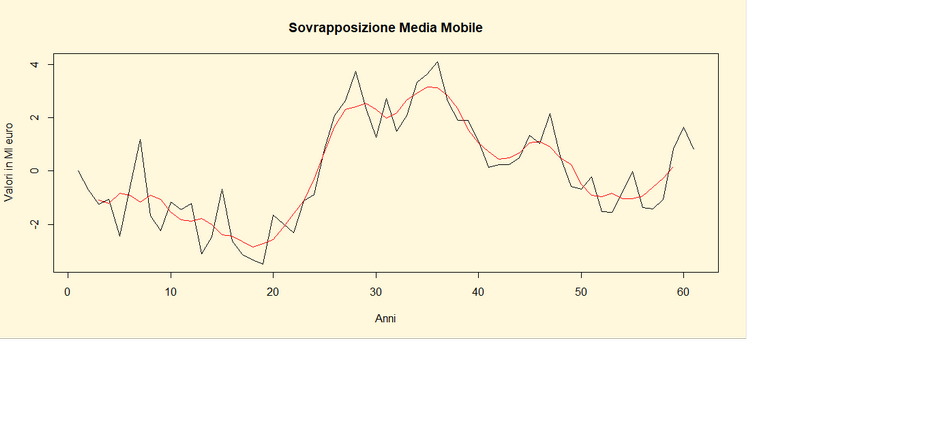
######## 2) SMUSSAMENTO CON MEDIE MOBILI DI ORDINE 5 ####################

dati.fil2<-filter(yt,filter=rep(1/5,5)); dati.fil2

par(bg="cornsilk")

ts.plot(yt,main="Sovrapposizione Media Mobile",xlab="Anni",ylab="Valori in Ml euro")

lines(dati.fil2, col="red")

##Risultato ##

Time Series:

Start = 1

End = 61

Frequency = 1

[1] NA NA -1.0896373 -1.2108906

[5] -0.8308849 -0.9173273 -1.1507912 -0.8947605

[9] -1.0634526 -1.5453441 -1.8281533 -1.8738843

[13] -1.7773000 -2.0121691 -2.3900512 -2.4377143

[17] -2.6413256 -2.8379385 -2.7107056 -2.5509450

[21] -2.1086571 -1.5879244 -1.0993827 -0.2859228

[25] 0.7033021 1.6713031 2.3163576 2.4097770

[29] 2.5382145 2.3103550 1.9825601 2.1783222

[33] 2.6513368 2.9247874 3.1490372 3.1110266

[37] 2.8260260 2.3271144 1.5374226 1.0624023

[41] 0.7322641 0.4504610 0.4932983 0.6719207

[45] 1.0540411 1.1121388 0.8963071 0.4902869

[49] 0.2383272 -0.4952148 -0.9111695 -0.9557564

[53] -0.8183696 -1.0434891 -1.0244484 -0.9277322

[57] -0.6042262 -0.2750185 0.1576087 NA

[61] NA

Si procede all’implementazione del modello additivo Holt-Winters implementando le seguenti linee di codice di R.

##Codice di R ##

######## 2) PREVISIONE CON LISCIAMENTO ESPONENZIALE ####################

dati.hw<-HoltWinters(yt, seasonal="additive");dati.hw

prev<-predict(dati.hw, n.ahead=15);prev

par(mfrow=c(2,1))

par(bg="cornsilk")

plot(dati.hw,main="Detrentizzazione Holt-Winters ",xlab="Anni",ylab="Valori in Ml euro")

plot(prev, main="Previsione 2012-2017")

##Risultato ##

Si procede ora alla simulazione dei diversi processi stocastici al fine di individuare quello più adatto. Iniziando da un white noise

##Codice di R ##

library(tseries)

yt <- arima.sim(list(order=c(0,0,0)), n=60); yt

par(bg="cornsilk")

ts.plot(yt, main="Simulazione processo stocastico white noise" ,lwd=5)

Si procede alla stima dei coefficienti del processo white noise

##Codice di R ##

library(tseries)

fit <- arima(lh, c(0,0,0)) ;fit

par(bg="cornsilk")

tsdiag(fit)

##Risultato ##

Coefficients:

intercept

2.4000

s.e. 0.0788

sigma^2 estimated as 0.2979: log likelihood = -39.05, aic = 82.09

Sia dall’esame visivo del grafico del processo che dalla diagnostica emerge che si rifiuta l’ipotesi nulla almeno per un valore di r relativo al ritardo fra 0 ed 1 ancorché il test di Ljung-Box sia statisticamente significativo. Si procede pertanto ad esaminare un altro processo ad esempio un AR(1) stimando dapprima i coefficienti

##Codice di R ##

library(tseries)

fit <- arima(lh, c(1,0,0)) ;fit

par(bg="cornsilk")

tsdiag(fit)

##Risultato ##

Call:

arima(x = lh, order = c(1, 0, 0))

Coefficients:

ar1 intercept

0.5739 2.4133

s.e. 0.1161 0.1466

sigma^2 estimated as 0.1975: log likelihood = -29.38, aic = 64.76

##Codice di R ##

library(tseries)

yt <- arima.sim(list(order=c(1,0,0)),ar.0.5739, n=60); yt

par(bg="cornsilk")

ts.plot(yt, main="Simulazione processo stocastico AR(1)" ,lwd=5)

##Codice di R ##

library(tseries)

fit <- arima(lh, c(1,1,0)) ;fit

par(bg="cornsilk")

tsdiag(fit)

##Risultato ##

Call:

arima(x = lh, order = c(1, 1, 0))

Coefficients:

ar1

-0.0404

s.e. 0.1443

sigma^2 estimated as 0.2525: log likelihood = -34.35, aic = 72.7

Si procede ora ad esaminare un altro processo ad esempio un MA(1) con costante stimando dapprima i coefficienti

##Codice di R ##

library(tseries)

fit <- arima(lh, c(0,0,1)) ;fit

par(bg="cornsilk")

tsdiag(fit)

Call:

arima(x = lh, order = c(0, 0, 1))

Coefficients:

ma1 intercept

0.4810 2.4051

s.e. 0.0944 0.0979

sigma^2 estimated as 0.2123: log likelihood = -31.05, aic = 68.1

Quindi si ottiene il grafico implementando le seguenti linee di codice:

##Codice di R ##

library(tseries)

yt <- arima.sim(list(order=c(0,0,1),ar=-0.0404,n=60); yt

par(bg="cornsilk")

ts.plot(yt, main="Simulazione processo stocastico MA(1)" ,lwd=5)

Si procede ora ad esaminare un altro processo ad esempio un ARMA(1,0,1) stimando dapprima i coefficienti

##Codice di R ##

library(tseries)

fit <- arima(lh, c(1,0,1)) ;fit

par(bg="cornsilk")

tsdiag(fit)

Call:

arima(x = lh, order = c(1, 0, 1))

Coefficients:

ar1 ma1 intercept

0.4522 0.1982 2.4101

s.e. 0.1769 0.1705 0.1358

sigma^2 estimated as 0.1923: log likelihood = -28.76, aic = 65.52

Quindi si ottiene il grafico implementando le seguenti linee di codice:

##Codice di R ##

library(tseries)

yt <- arima.sim(list(order=c(1,0,1),ar1=0.4522,ma1=0.1982),n=60); yt

par(bg="cornsilk")

ts.plot(yt, main="Simulazione processo stocastico ARMA(1,1)" ,lwd=5)

Infine si procede ora ad esaminare un altro processo ad esempio un ARIMA(1,1,1) stimando dapprima i coefficienti

##Codice di R ##

library(tseries)

fit <- arima(lh, c(1,1,1)) ;fit

par(bg="cornsilk")

tsdiag(fit)

Call:

arima(x = lh, order = c(1, 1, 1))

Coefficients:

ar1 ma1

0.6060 -0.9919

s.e. 0.1383 0.3126

sigma^2 estimated as 0.2033: log likelihood = -30.34, aic = 66.68

Quindi si ottiene il grafico implementando le seguenti linee di codice:

##Codice di R ##

library(tseries)

yt <- arima.sim(list(order=c(1,1,1),ar1=0.6060,ma1= -0.9919),n=60)<yt

par(bg="cornsilk")

ts.plot(yt, main="Simulazione processo stocastico ARIMA(1,1,1)" ,lwd=5)

#################################################

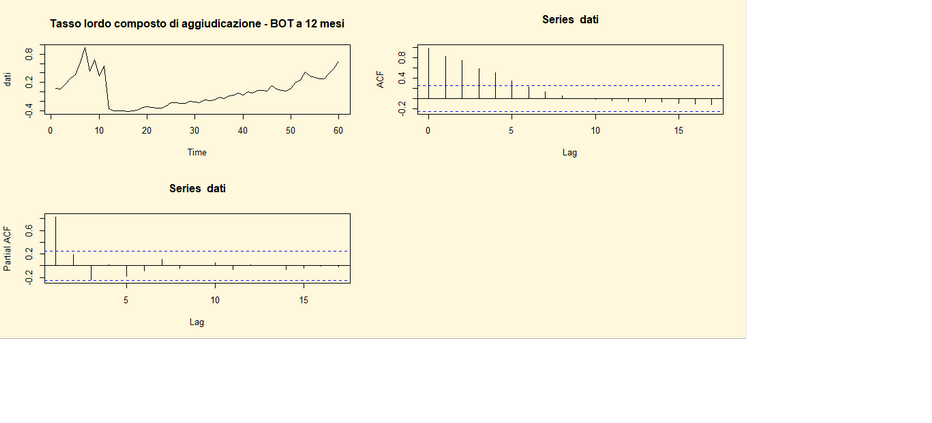
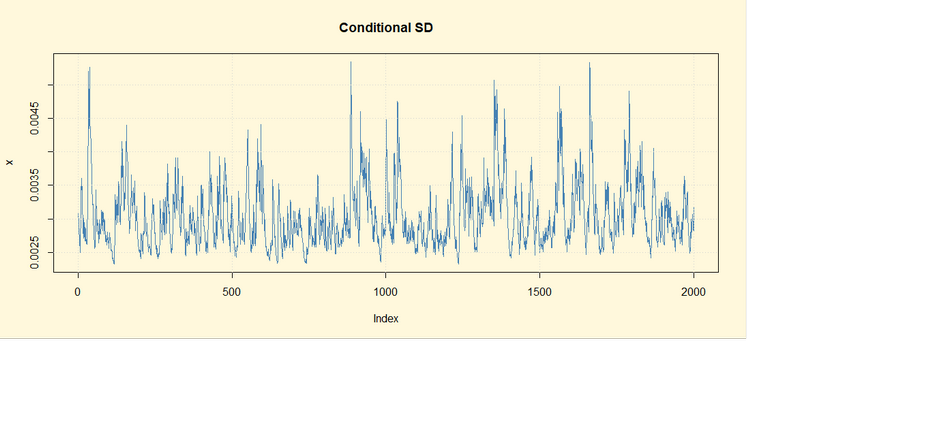
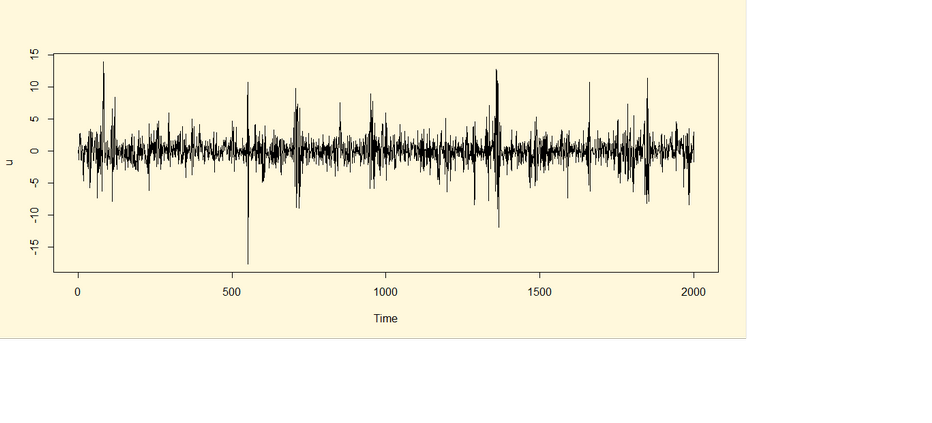
APPUNTI PER LEZIONE DEL 21 E 22 MAGGIO 2019

Introduzione

La modellizzazione e la previsione della volatilità dei mercati azionari è stata uno degli argomenti principali dell'econometria finanziaria negli ultimi anni. Lo scopo dello studio è di valutare le prestazioni di previsione dei modelli di tipo GARCH in termini di campioni e in accuratezza delle previsioni al di fuori del campione. I modelli ARCH hanno le loro radici in uno studio di Robert Engle (1982) e sono stati generalizzati (GARCH) da Bollerslev (1986) e Taylor (1986), diventando strumenti estremamente utili nell'econometria finanziaria applicata. Questi modelli sono stati ulteriormente ampliati per coprire l'impatto asimmetrico (o effetto leva) dei rendimenti sulla volatilità e la proprietà di memoria lunga nella volatilità.

Per catturare l'asimmetria della volatilità, Nelson (1991) ha sviluppato il modello esponenziale di GARCH

(EGARCH). Una panoramica dei modelli GARCH utilizzati nell'analisi è presentata nella tabella 1 (vedi Per un'ampia revisione delle previsioni di volatilità i modelli sviluppati negli ultimi anni sono quelli di Poon & Granger(2003), Xiao & Aydemir (2007) e Andersen et al. (2006a, b). Per eseguire una valutazione più approfondita sono state scelte come possibili distribuzioni

del termine di errore la funzione di distribuzione normale, la distribuzione di Student-t e la GDE (Generation Error Distribution).

I modelli GARCH sono stati anche valutati in base alla loro capacità di previsione dei rendimenti futuri. Sono stati calcolati gli indicatori più significativi quali l’ errore quadratico medio (RMSE), l’errore assoluto medio (MAE), la media assoluta percentuale dell’errore (MAPE) e il loro coefficiente di disuguaglianza (TIC).

Si vuole applicare il modello GARCH alla serie storica del tasso loro di aggiudicazione dei BOT a 12 mesi composta da 60 osservazioni relative al periodo maggio 2014 - aprile 2019.

La prima parte del campione, costituita da 50 osservazioni (maggio 2014 - giugno 2018), è stato utilizzato per calcolare le statistiche riassuntive dei ritorni e per la stima dei modelli GARCH.

La seconda parte del campione, consistente in 10 osservazioni (dal luglio 2018 all’aprile 2019), è stata lasciata all'esame dell'affidabilità della previsione al di fuori del campione. Si riportano di seguito i 60 valori campionari.

Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec

2014 0.070 0.060 0.181 0.285 0.370 0.630 0.949 0.436

2015 0.679 0.337 0.550 -0.361 -0.399 -0.403 -0.401 -0.420 -0.407 -0.395 -0.334 -0.326

2016 -0.337 -0.352 -0.351 -0.304 -0.239 -0.226 -0.247 -0.250 -0.196 -0.217 -0.238 -0.175

2017 -0.190 -0.176 -0.122 -0.140 -0.081 -0.068 -0.032 -0.074 -0.003 -0.030 0.023 0.028

2018 0.011 0.124 0.061 0.027 0.013 0.079 0.209 0.243 0.418 0.335 0.301 0.271

2019 0.279 0.387 0.495 0.650

Si riportano di seguito le linee di codice per rappresentare graficamente la serie storica e le funzioni di autocorrelazione totale e parziale.

##CODICE DI R##

library(tseries)

dati<-c(0.070, 0.060, 0.181, 0.285, 0.370, 0.630, 0.949, 0.436, 0.679,

0.337, 0.550, -0.361, -0.399, -0.403, -0.401, -0.420, -0.407, -0.395,

-0.334, -0.326, -0.337, -0.352, -0.351, -0.304, -0.239, -0.226, -0.247,

-0.250, -0.196, -0.217, -0.238, -0.175, -0.190, -0.176, -0.122, -0.140,

-0.081, -0.068, -0.032, -0.074, -0.003, -0.030, 0.023, 0.028, 0.011,

0.124, 0.061, 0.027, 0.013, 0.079, 0.209, 0.243, 0.418, 0.335,

0.301, 0.271, 0.279, 0.387, 0.495, 0.650)

par(mfrow=c(1,2))

par(bg="cornsilk")

ts.plot(dati,main="Tasso lordo composto di aggiudicazione - BOT a 12 mesi")

acf(dati)

pacf(dati)

Nel grafico seguente vengono rappresentate la serie storica e le due funzioni di autocorrelazione totale e parziale.

Si riportano le linee di codice per calcolare i parametri e per rappresentare graficamente un processo GARCH(1,1) con 2000 replicazioni

##CODICE DI R##

library(fGarch)

garch_micro = garchSim(n = 2000)

garch_fit <- garchFit(Formula= ~garch(1, 1), data = garch_micro, trace = FALSE)

par(bg="cornsilk")

plot(garch_fit, which=2)

##RISULTATO##

Conditional Distribution:

norm

Coefficient(s):

mu omega alpha1 beta1

-8.4112e-05 1.1971e-06 1.1615e-01 7.5844e-01

Std. Errors:

based on Hessian

Error Analysis:

Estimate Std. Error t value Pr(>|t|)

mu -8.411e-05 6.398e-05 -1.315 0.189

omega 1.197e-06 2.854e-07 4.195 2.73e-05 ***

alpha1 1.161e-01 2.175e-02 5.341 9.23e-08 ***

beta1 7.584e-01 4.196e-02 18.077 < 2e-16 ***

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Log Likelihood: 8774.671 normalized: 4.387336

Si riportano le linee di codice per calcolare i parametri e per rappresentare graficamente un processo GARCH(1,1) con 2000 replicazioni e con coefficienti mu=0.8, omega=0.5, alpha1=0.4, beta1=0.1.

##CODICE DI R##

library(fImport)

library(fGarch)

library(tseries)

n = 2000

coeff = c(0.8,0.5,0.4,0.1)

coeff0 = coeff[1]

coeff = coeff[-1]

l = length(coeff)

u = double(n)

u[1:l] = coeff0 * rnorm(l)

for (i in (l+1):n) {

u[i] = sqrt( coeff0 + sum(coeff * u[(i-1):(i-l) ]^2 )) * rnorm(1)

}

u = ts(u)

ts.plot(u)

Modelli autoregressivi vettoriali per Serie temporali multivariate (VAR)

Il modello di autoregressione vettoriale (VAR) è uno dei più riusciti, flessibile e facili da usare per l'analisi di serie

temporali multivariate. È una naturale estensione del modello autoregressivo che da univariato diventa multivariato

dinamico. Il modello VAR ha dimostrato di essere particolarmente utile per descrivendo il comportamento dinamico delle

serie temporali economiche e finanziarie soprattutto ai fini della previsione. Spesso fornisce previsioni

superiori a quelle dei modelli univariati basati sull’elaborazione di equazioni simultanee. Le previsioni dei

modelli VAR sono piuttosto flessibili perché si adattano ai potenziali percorsi futuri delle variabili

specificate nel modello. Oltre alla descrizione e alla previsione dei dati, il modello VAR è anche utilizzato per l'inferenza

strutturale e l'analisi delle politiche. Nell'analisi strutturale sono imposte alcune ipotesi sulla struttura causale dei dati in

esame legate a possibili shock imprevisti o innovazioni relativi alle variabili specificate nel modello. Questi impatti causali

sono di solito riassunti con la funzione di risposta all'impulso e con previsioni sulla scomposizione della varianza

dell'errore. Questo capitolo si concentra sull'analisi della covarianza stazionaria multivariata

Esempio. Si simula un processo stocastico autoregressivo vettoriale multivariato stazionario VAR(1) usando le linee di

codice di R composto da 250 osservazioni

y1t = −0.7 + 0.7y1t−1 + 0.2y2t−1 + ε1t

y2t = 1.3 + 0.2y1t−1 + 0.7y2t−1 + ε2t

con

Π₁ = 0.4 0.3 c= -0.7 μ= 0.3 Σ = 1 0.5

0.35 0.2 1.3 -2.8 0.5 1

e gli errori distribuiti normalmente.

## CODICE DI R ##

library(vars)

library(MASS)

mu <- c(0.3, -2.8)

sigma.var <- diag(1, 2)

A1 = matrix(c(0.4, 0.35, 0.3, 0.2), 2, 2, byrow = TRUE)

E <- mvrnorm(1500, mu, sigma.var)

Y <- matrix(0, 1500, 2)

colnames(Y) <- c("y1", "y2")

for (i in 2:1500) {Y[i, ] <- A1 %*% Y[i - 1, ] + E[i, ]}

est.sim.var <- VAR(Y, type = "const", lag = 1)

coef(est.sim.var)

## RISULTATO ##

$y1

Estimate Std. Error t value Pr(>|t|)

y1.l1 0.3722231 0.02217752 16.783799 4.659708e-58

y2.l1 0.3565055 0.02432765 14.654331 1.543247e-45

const 0.2946987 0.10652664 2.766432 5.737063e-03

$y2

Estimate Std. Error t value Pr(>|t|)

y1.l1 0.3208118 0.02132259 15.045629 9.532970e-48

y2.l1 0.2248364 0.02338984 9.612567 2.870901e-21

const -2.6786285 0.10242011 -26.153346 1.775086e-124

I tre criteri di informazione più comuni sono i

Akaike (AIC), Schwarz-Bayesian (BIC) e Hannan-Quinn (HQ)

Molte delle considerazioni che abbiamo fatto in precedenza a proposito dei modelli AR si estendono in modo piuttosto banale ai modelli VAR. Il fatto che però in un modello multivariato abbiamo a che fare con dei polinomi matriciali anziché scalari impone una serie di considerazioni aggiuntive. Tanto per cominciare, possiamo chiederci se è possibile, come nel caso univariato, esprimere un processo VAR in forma di processo a media mobile multivariato (VMA). La risposta è evidentemente legata all’invertibilità dell’operatore A(L), il che ci porta a valutare sotto quali condizioni A(L) possieda un’inversa. In questo caso siamo in presenza di un polinomio matriciale di primo grado. Prendiamo un AR(2) la cui notazione viene espressa di seguito:

y_t = 1.3y_t−1− 0.4y_t−2+ e_t

allora il polinomio di cui dobbiamo trovare le radici è A(z) = 1 − 1.3z + 0.4z ed essendo di secondo grado si applica la classica notazione per il calcolo delle radici:

z=+1,3±RDAQ(1,3² -2*1*1.3)/2*0,4=> z₁ = 2

z₂ = 1,25

essendo entrambi i valori delle radici maggiori di 1 il processo è stazionario.

Si può affermare che un processo stocastico a radice unitaria è definito random walk ed è non stazionario.

Un processo stocastico AR(2) come quello esaminato sopra si può trasformare in un VAR(1) e si può dimostrare che è stazionario in covarianza se gli autovalori del polinomio matriciale sono minori di 1 in valore assoluto. In questo caso la matrice per il calcolo diverrebbe:

1.3 – λ -0.4

1 - λ

Sviluppando matematicamente la matrice si ottengono due valori: λ₁ = 0.8 => si noti che λ₁=1/z₂

Λ₂ = 0.5 => si noti che λ₂=1/z₁

Le linee di codice di R per calcolarli sono:

A <-matrix(data = c(1.3, 1, -0.4, -1), nrow = 2, ncol = 2); A

n <- 2

A <- diag(eigen(A)$values); A

GAMMA <- eigen(A)$vectors; GAMMA

UNIVERSITA’ DEGLI STUDI DI FOGGIA DIPARTIMENTO DI ECONOMIA

Esercitazione di ECONOMETRIA

del 21/05/2019

Prof. Raoul COCCARDA

Sezione 1 – Domande a risposta multipla

1) Quali sono i momenti di un processo stocastico intesi in senso lato

valore atteso, varianza a

valore atteso, varianza, autocovarianza b

valore atteso, varianza, autocovarianza e autocorrelazione c

valore atteso, devianza, autocovarianza e autocorrelazione d

2) Un processo stocastico può essere stazionario:

in senso debole a

in senso debole e in senso forte o stretto b

in senso debole e diretto c

in senso forte e indiretto d

3) La stazionarietà debole può essere definita anche come:

stazionarietà in covarianza a

stazionarietà in autocorrelazione b

stazionarietà in valore atteso c

stazionarietà in varianza d

4) Con quale script si ottengono 10 numeri casuali da una binomiale con p=0.12 e n=13 e 15 da una normale con valore atteso pari a 1.5 e varianza pari a 0.9:

rbinom(10,13,0.12);rnorm(15,1.5,sqrt(0.9)) a

rbinom(13,0.12);rnorm(15,1.5,0.9) b

rbinom(10,13,0.12);rnorm(,1.5,sqrt(0.9)) c

rbinom(10,13);rnorm(15,1.5,sqrt(0.9)) d

5) Quale è la notazione che esprime un processo stocastico “white noise” :

Autocovarianza: σ²per k=0; 0 per k≠0 Autocorrelazione totale e parziale: 1 per k=0; 0 per k≠0 a

Autocovarianza: σ²per k=1; 0 per k≠0 Autocorrelazione totale e parziale: 1 per k=0; 0 per k≠0 b

Autocovarianza: σ²per k=0; 0 per k≠0 Autocorrelazione parziale: 1 per k=0; 0 per k≠0 c

Autocovarianza: σ²per k=0; 0 per k≠0 Autocorrelazione totale e parziale: 0 per k=1; 0 per k≠0 d

6) Quale è la notazione che esprime un processo stocastico AR(1):

Y_t=φ₀+ φ₁ Y_t-₁a

Y_t=φ₀+ φ₁ Y_t-₁+ є_tb

Y_t=φ₀+ φ₁ Y_t+ є_tc

Y_t=φ₀+ Y_t-₁+ є_td

7) Quale è la notazione che esprime un processo stocastico MA(1):

Y_t=є_t-1 + θ₁є_t-1a

Y_t=є_t + θ0є_t-1b

Y_t=є_t + θ₁є_tc

Y_t=є_t + θ₁є_t-1d

8) Quali linee di codice si implementano per rappresentare graficamente un processo stocastico AR(1) con coefficiente ar=0.48:

library(tseries);ar1<-arima.sim(n=1,0,0,list(c(1,0,0),ar=0.48));ar1 a

library(tseries);ar1<-arima.sim(n=1,0,0,list(order=c(1,0,0),ar=0.48)) b

library(tseries);ar1<-arima.sim(n=1,0,0,list(order=c(1,0,0),ar=0.48));ar1 c

library(tseries);ar1<-arima.sim(n=1,0,0,list(order=c(1,0,0),ar=0.48));ar1 d

9) Quali linee di codice di R si implementano per calcolare i coefficienti compresa l’intercetta di un processo stocastico MA(1):

library(tseries); fit <- arima(lh, c(0,0,1)) ;fit a

library(tseries); fit <- arima(lh, c(0,0,1)) ;fit b

library(tseries); fit <- arima(lh, c(0,0,1)) ;fit c

library(tseries); fit <- arima(lh, c(0,0,1)) ;fit d

10) Quali linee di codice di R si implementano per calcolare i coefficienti senza l’intercetta di un processo stocastico AR(1) e rappresentare la relativa diagnostica:

library(tseries); fit <- arima(lh, c(1,0,1)) ;fit a

library(tseries); fit <- arima(lh, c(0,0,0)) ;fit b

library(tseries); fit <- arima(lh, c(0,0,1)) ;fit c

library(tseries); fit <- arima(lh, c(1,1,0)) ;fit d

11) Quante sono le tipologie di correlogramma studiate e quali sono le componenti che possono prevalere:

tre; 1. componente trend; 2. componente stagionale; 3. componente erratica o casuale a

due; 1. componente trend; 2. componente stagionale b

tre; 1. componente diretta; 2. componente stagionale; 3. componente erratica o casuale c

tre; 1. componente trend; 2. componente indiretta; 3. componente erratica o casuale d

Sezione 2 – Domande a risposta aperta

Domanda aperta 1. Date le due rappresentazioni grafiche delle finzioni di autocorrelazione totale e parziale:

a) definire sinteticamente del due funzioni e mettere in evidenza le differenze; b) spiegare perché il valore di r per il ritardo 0 è sempre uguale a 1; c) spiegare a quale tipologia appartengono i due correlogrammi d); spiegare il significato di lag riportato in ascissa e scrivere e commentare le linee di codice di R coerenti con l’argomento

Domanda aperta 2. A proposito di un processo stocastico white noise:

a) presentare un esempio di un processo white noise e definirlo; b) scrivere le notazioni dei momenti che lo contraddistinguono; c) spiegare come intervengono nelle notazioni dei processi AR(p) e MA(q); d); scrivere e commentare le linee di codice di R coerenti con l’argomento

Domanda aperta 3. A proposito di un processo stocastico AR(1):

a) presentare un esempio di un processo AR(1) e definirlo; b) scrivere le notazioni dei momenti che lo contraddistinguono; c) spiegare come si calcolano i coefficienti di autocorrelazione; d); scrivere e commentare le linee di codice di R coerenti con l’argomento

Domanda aperta 4. A proposito di un processo stocastico MA(1):

a) presentare un esempio di un processo MA(1) e definirlo; b) scrivere le notazioni dei momenti che lo contraddistinguono ; c) spiegare come si calcolano i coefficienti di autocorrelazione; d); scrivere e commentare le linee di codice di R coerenti con l’argomento

Domanda aperta 5. A proposito di un processo stocastico ARMA(1,1):

a) presentare un esempio di un processo ARMA(1,1) e definirlo; b) spiegare perché il valore di r per il ritardo 0 è sempre uguale a 1; c) spiegare d); scrivere e commentare le linee di codice di R coerenti con l’argomento

#####################################################################

DIPARTIMENTO DI ECONOMIA UNIVERSITA’ DEGLI STUDI DI FOGGIA

Prova in itinere di econometria del 28/05/2019

Domande a risposta multipla (quattro risposte di cui una sola corretta)

1) Con quali linee di codice si ottiene l’output della regressione lineare semplice con R:

a) modello<-(y~x); summary(modello)

b) modello<-lm(y~x); summary(modello)

c) modello<-lm(y~x); summary

d) modello<-lm(y+x); summary(modello)

2) Con quale linea di codice si calcola il quantile della F critica per un test bilatero con un livello di significatività alfa=0.05 con 11 gradi di libertà al numeratore e 15 al denominatore:

a) F_critica<-qf(1-0.05/2,11,15);F_critica

b) F_critica<-qf(1-0.05, 11,15);F_critica

c) F_critica<-qf(0.05, 11,15);F_critica

d) F_critica<-qf(1-0.05, 11,15);F_critica

3) Con quali linee di codice si calcolano i p-value, dati i valori dei quantili empirici della t di Student pari a -2.228 e 1,23, per un test bilatero con 11 gradi di libertà:

a) p-value<-(pt(-2.228,11));p_value - p-value<-(1-pt(1.23, 11));p_value

b) p-value<-2*(pt(-2.228,11));p_value - p-value<-2*(1-pt(1.23, 11));p_value

c) p-value<-2*(pt(-2.228));p_value - p-value<-2*(1-pt(1.23,));p_value

d) p-value<-2*(pt(-2.228,11));p_value - p-value<-2*(pt(1.23, 11));p_value

4) Il termine di errore del MRLM ε sottostà a quali ipotesi di base:

a) è una v.c. i.i.d. con E(ε)=0; Var (ε_i )= I ;Cov(ε_i ε_j)=0; ε_i~ N(μ,ϭ² I)

b) è una v.c. i.i.d. con E(ε)=0; Var (ε_i )= ; Cov(ε_i ε_j)=0

c) è una v.c. i.i.d. con E(ε)=0; ; Cov(ε_i ε_j)=0; εi ~ N(μ,ϭ²)

d) è una v.c. i.i.d. con E(ε)=0; εi ~ N(μ,ϭ2)

5) Con quale formula si calcola la statistica-test F di Fisher

a) F= MDS/MDR

b) F= MDT/MDR

c) F= MDS/MDR

d) F= MDS/MDT

6) Come si esprime in forma matriciale o compatta l’equazione del Modello di Regressione lineare multipla

a) Y=βX+є

b) Y=βX

c) Y=X+є

d) Y=β+є

7)Quale linea di codice di R si utilizza per calcolare gli indicatori C,alpha e DG.rho in un modello di regressione a variabili latenti per il data frame df

a) library(“plspm”); satpls<-plspm(df,sat.inner,sat.outer,sat.mod, scheme=”centroid”;scaled=TRUE) (satpls)

b) library(“plspm”); satpls<-plspm(df,sat.inner,sat.outer,sat.mod, scheme=”centroid”) summary(satpls)

c) library(“plspm”); satpls<-plspm(df,sat.inner,sat.outer,sat.mod, scaled=TRUE) summary(satpls)

d) library(“plspm”); satpls<-plspm(df,sat.inner,sat.outer,sat.mod, scheme=”centroid”;scaled=TRUE) summary(satpls)

8) Come può essere la probabilità a priori.

a) Informativa – Non informativa o di Jeffreys

b) Informativa

c) Non Informativa

d) Nulla

9) Dato il seguente output di R del GQ Test = 0.49451, df1 = 14, df2 = 14, p-value = 0.9 e il sistema di ipotesi quale sarà la regola di decisione

F= H0:assenza di etroschedasticità vs H1:presenza di eteroschedasticità; Si RIFIUTA H0 sotto H1

F= H0:assenza di etroschedasticità vs H1:presenza di eteroschedasticità; Si ACCETTA H1 sotto H0

F= H0:assenza di etroschedasticità vs H1:presenza di eteroschedasticità; Si ACCETTA H1

F= H0:assenza di etroschedasticità vs H1:presenza di eteroschedasticità; Si ACCETTA H0 sotto H1

10) Dato un modello a due covariate x1 e x2 ed una intercetta quale è la notazione con una variabile dummy D legata alla x2:

a) Y= b₀+b₁x1+ b₂x2+є

b) Y= b₀+b₁x1+ Db₂+є

c) Y= b₀+b₁x1+ Dx2+є

d) Y= b₀+b₁x1+ b₂Dx2+є

11) Dato un modello ad una covariata x ed una intercetta quale è la notazione di un modello log-log

a) logY= b₀+b₁logx+є

b) Y= b₀+b₁logx+є

c) logY= b₀+b₁x+є

d) logY= b₀+b₁logx

Domande a risposta aperta.

1. Da una indagine statistica bivariata sono stati rilevati i seguenti dati 0, 0, 1, 2, 3, 2, 1,2, 2 del carattere X che assume le modalità (alto, medio, basso) e del carattere Y che assume le modalità (1,2,3) e si vuole: a) implementare il codice per costruire la relativa matrice; b) redigere la tabella a doppia entrata delle frequenze congiunte assolute; c) redigere la tabella a doppia entrata delle frequenze teoriche; d) redigere la tabella a doppia entrata delle contingenze assolute.

2. Dato il seguente output di R: Call:

lm(formula = y ~ x1 + x2)

Residuals:

1 2 3 4 5

-1.03300 -0.03844 0.44435 0.14229 0.48479

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 2.468 2.237 1.103 0.3849

x1 16.676 3.214 5.189 0.0352 *

x2 17.221 15.932 1.081 0.3928

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8721 on 2 degrees of freedom

Multiple R-squared: 0.9344, Adjusted R-squared: 0.8689

F-statistic: 14.25 on 2 and 2 DF, p-value: 0.06557

a) si può affermare se l’ipotesi di linearità è confermata e quali procedure si devono implementare per verificarla; b) stabilire se il modello è affetto da multicollinearità; c) stabilire se il modello è affetto da eteroschedasticità; d) verificare l’ipotesi di normalità degli errori

3. Data la seguente serie storica dei prezzi medi mensili di una azione: Gen 201,3 Feb 200,08 Mar 201,9 Apr 199,78 Mag 200,01

Giu 198,99 Lug 201,5 Ag 200,00 Sett 201,6 Ott 200,3 Nov 199,1 Dic 199,8 calcolare: a) la media mobile a cinque termini; b) le linee di codice di R per implementare la media mobile di cui al punto a); c) le linee di codice di R per implementare il modello additivo Holt-Winters; d) le linee di codice per prevedere i prezzi dei 6 mesi successivi

4. Data una serie storica: a) con quale notazione viene espresso un processo stocastico MA(1) e quali linee di codice di R si implementano per calcolarlo senza intercetta; b) con quale notazione viene espresso un processo stocastico AR(1) e quali linee di codice di R si implementano per calcolarlo con intercetta; c) a) con quale notazione viene espresso un processo stocastico ARMA(1,1) e quali linee di codice di R si implementano per calcolarlo; d) quali linee di codice di R si implementano per calcolare i coefficienti del modello di cui al punto b)

5. Data la seguente notazione con cui si esprime un processo stocastico AR(2): y_t = 1.3y_t−1− 0.4y_t−2+ e_t : a) calcolare le radici del polinomio; b) rappresentare la matrice degli autovalori; c) quali linee di codice di implementano per calcolare gli autovalori della matrice (1.3, 1, -0.4, 0); d) che relazione esiste fra le radici del polinomio e gli autovalori

############################

Prova in itinere di Econometria 29 maggio 2019

DOMANDE A RISPOSTA MULTIPLA

1. Data la notazione del MRLM Y=IXβ+ϵ cosa sta a rappresentare X.

a) la matrice delle variabili indipendenti per n osservazioni campionarie e k regressori

b) la matrice delle variabili indipendenti per n osservazioni e k regressori

c) la matrice delle variabili dipendenti per n osservazioni campionarie e k regressori

d) la matrice delle variabili indipendenti per n osservazioni campionarie

2. L’ipotesi di indipendenza degli errori come può essere specificata

a) che il vettore della v.c. ϵ è composto da valori campionari identicamente distribuiti (i.i.d.)

b) che il vettore della v.c. ϵ è composto da valori campionari indipendenti e identicamente distribuiti (i.i.d.)

c) che la matrice della v.c. ϵ è composta da valori campionari indipendenti e identicamente distribuiti (i.i.d.)

d) che il vettore della v.c. Y è composto da valori campionari indipendenti e identicamente distribuiti (i.i.d.)

3. Data la notazione del vettore dei regressori stimato del MRLM b =(X’X)^-1 X’y cosa sta a rappresentare (X’X)^-1.

a) la matrice delle variabili indipendenti per n osservazioni campionarie e k regressori

b) la matrice di correlazione

c) la matrice di varianze-covarianze inversa

d) la matrice delle variabili indipendenti per n osservazioni campionarie

4. Con quale notazione si esprime la varianza del vettore dei parametri stimato b in un modello affetto da eteroschedasticità.

a) var(b) =(X’X)^-1 XΩ (X’X)^-1

b) var(b) =σ²(X’X)^-1 X’(X’X)^-1

c) var(b) = σ² (X’X)^-1 X’X(X’X)^-1

d) var(b) = σ² (X’X)^-1 X’ΩX(X’X)^-1

5. Con quale notazione si calcola il VIF di un MRLM con due covariate x1 e x2; quale libreria e linea di codice si implementa per calcolarlo:

a) VIF=1/1-R² ; library(faraway);modello<-lm(y~x1+x2); vif(modello)

b) VIF=1/1+R² ; library(faraway);modello<-lm(y~x1+x2); vif(modello)

c) VIF=1/1-R² ; modello<-lm(y~x1+x2); vif(modello)

d) VIF=1/1-R² ; library(faraway);modello<-lm(y~x1-x2); vif(modello)

6. Dati i valori del VIF di un MRLM a due covariate x1=24.576 e x2=22.671 si accetta o si rifiuta l’ipotesi nulla; quale sistema di ipotesi si implementa

a) si accetta se il sistema di ipotesi è: H₀ : presenza vs H₁:assenza

b) si rifiuta se il sistema di ipotesi è: H₀ : presenza vs H₁:assenza

c) si accetta se il sistema di ipotesi è: H₀ : assenza vs H₁:presenza

d) si accetta se il sistema di ipotesi è: H₁ : presenza vs H₁:assenza

7. Quale è la notazione che specifica il modello probit

a) P(Y=1|x)=(β₀ + β₁ X)

b) P(Y=1|x)=Φ(β₀ - β₁ X)

c) P(Y=1|x)=Φ(β₀ + X)

d) P(Y=1|x)=Φ(β₀ + β₁ X)

8. Cosa sta a rappresentare Φ nella notazione di cui alla domanda 7

a) la funzione di ripartizione di una v.c. normale standardizzata

b) la funzione di ripartizione di una v.c. t di Student

c) la funzione di ripartizione di una v.c. Chi-quadrato

d) la funzione di ripartizione di una v.c. F di Fisher

9. Data la notazione del MRLM Y=IXβ+ϵ cosa sta a rappresentare X.

a) la matrice delle variabili indipendenti per n osservazioni campionarie e k regressori

b) la matrice delle variabili indipendenti per n osservazioni e k regressori

c) la matrice delle variabili dipendenti per n osservazioni campionarie e k regressori

d) la matrice delle variabili indipendenti per n osservazioni campionarie

10. Dati tre modelli con R²rispettivamente uguale a 0.911; 0,877 e 0,821 quale dei tre si adatta meglio ai dati

a) il primo

b) il secondo

c) il terzo

d) nessuno

11. Quando si utilizza il modello a variabili strumentali e quali sono le condizioni base a cui deve sottostare

a) quando la variabile dipendente Y è in parte correlata ed in parte non correlata con il termine di errore ϵ; la condizione base è quella della rilevanza

b) quando la variabile esplicativa X è in parte correlata con il termine di errore ϵ; le condizioni base sono quelle della rilevanza e dell’esogeneità

c) quando la variabile esplicativa X è in parte non correlata con il termine di errore ϵ; le condizioni base sono quelle della rilevanza e dell’esogeneità

d) quando la variabile esplicativa X è in parte correlata ed in parte non correlata con il termine di errore ϵ; le condizioni base sono quelle della rilevanza e dell’esogeneità

Domande a risposta aperta

1. Si scelga una serie storica con dati a piacere e si calcoli:

il primo termine di una media mobile a 5 termini centrata; b) si implementi il relativo codice di R; Il primo termine di Si scelga una media mobile con dati a piacere e si calcoli:

a) Il primo termine di una media mobile a 5 termini centrata; b) si implementi il relativo codice di R; c)l primo termine di una media mobile a 3 termini centrata; d) si implementi il relativo codice di R

2. Della serie storica di cui alla domanda 1 si scriva:

a) si scriva la notazione del modello additivo; b) si scriva la notazione del modello moltiplicativo; c) si definisca e si commenti la componente trend; d) si definisca e si commenti la componente stagionalità

3. Data una serie storica:

rappresentare il relativo correlogramma dove prevale la componente trend; b) rappresentare il relativo correlogramma dove prevale la componente stagionalità; c) rappresentare il relativo correlogramma dove prevale la componente erratica; d) definire il correlogramma

4. Data una serie storica:

a) definire la funzione di autocorrelazione totale; b) definire la funzione di autocorrelazione parziale; c) come si calcola il ritardo 0 nella funzione di autocorrelazione totale; d) definire sinteticamente il concetto di ritardo

5. Dato un processo stocastico scelto a piacere:

b) scrivere la notazione del primo momento; b) scrivere la notazione del secondo momento; c)scrivere la notazione del terzo momento; d) scrivere la notazione del quarto momento

#######################################

Prova in itinere di Econometria 30 maggio 2019

DOMANDE A RISPOSTA MULTIPLA

1. Data la matrice X_5x2 quali sono le linee di codice di R per ottenere (X’_2x5 X_5x2)^-1_2x2

a) D<-t(X);C<-D%*%X;N<-solve(C);N

b) D<-t(X);C<-D*%X;N<-solve(C);N

c) D<-t(X);C<-D%*%X;N<-(C);N

d) D<-(X);C<-D%*%X;N<-solve(C);N

2. Con quale linea di codice di R si calcolano i test GQ e BP per la verifica dell’ipotesi di omoschedasticità in un MRLM con due covariate

a) library(lmtest);modello<-lm(y~x1-x2); gqtest(modello); bptest(modello)

b) library(lmtest);modello<-lm(y~x1+x2); gqtest(modello) ; bptest(modello)

c) library(lmtest);modello<-lm(y~x1+x2); test(modello) ; bptest(modello)

d) library(lmtest);modello<-l(y~x1+x2); gqtest(modello) ; bptest(modello)

3. Con quale linea di codice di R si calcola l’ANOVA in un MRLM con due covariate

a) library(labstatR);modello<-lm(y~x1-x2); anova(modello)

b) library(labstatR);<-lm(y~x1-x2); anova(modello)

c) library(labstatR);modello<-lm(y~x1-x2); anova(modello)

d) library(labstatR);modello<-lm(y~x1-x2); anova

4. In un modello di regressione a struttura latente cosa mette in evidenza il modello esterno (outer model)

a) i valori relativi ai pesi, al caricamento, alla comunalità per ciascuna variabile latente

b) i valori relativi ai pesi, al caricamento e alla ridondanza per ciascuna variabile latente

c) i valori relativi ai pesi, alla comunalità e alla ridondanza per ciascuna variabile latente

d) i valori relativi ai pesi, al caricamento, alla comunalità e alla ridondanza per ciascuna variabile latente

5. Dato il seguente output di R del GQ Test = 0.49451, df1 = 14, df2 = 14, p-value = 0.9 quale sistema di ipotesi si imposta per la presenza e l’assenza di eteroschedasticità e quale sarà la regola di decisione:

a) H₀:assenza di etroschedasticità vs H₁:presenza di eteroschedasticità; Si rifiuta H₀ sotto H₁

b) H₀:assenza di etroschedasticità vs H₁:presenza di eteroschedasticità; Si accetta H₁ sotto H₀

c) H₀:assenza di etroschedasticità vs H₁:presenza di eteroschedasticità; Si accetta H₁

d) H₀:assenza di etroschedasticità vs H₁:presenza di eteroschedasticità; Si accetta H₀ sotto H₁

6. I pilastri su cui si fonda la statistica bayesiana sono

a) due; il primo è l’utilizzo del teorema di Bayes e il secondo è la definizione di un modello che minimizzi il rischio

b) tre; il primo è l’utilizzo del teorema di Bayes e il secondo è la definizione di un modello che minimizzi il rischio

c) due; il primo è l’utilizzo del teorema di Bernoulli e il secondo è la definizione di un modello che minimizzi il rischio

d) due; il primo è l’utilizzo del teorema di Bayes e il secondo è la definizione di un modello che massimizzi il rischio

7. Quando si utilizza il modello di regressione robusto e quale metodo adotta

a) quando si è in presenza di valori anomali e il metodo è quello dei minimi quadrati ponderati

b) quando non si è in presenza di valori anomali e il metodo è quello dei minimi quadrati ponderati ripetuti (IRLS)

c) quando si è in presenza di valori anomali e il metodo è quello dei minimi quadrati ordinari (OLS)

d) quando si è in presenza di valori anomali e il metodo è quello dei minimi quadrati ponderati ripetuti (IRLS)

8. Un modello di regressione con dati panel è definito ad effetti fissi quando

a) la componente degli errori è un parametro non noto e non influenzato dalla sua natura casuale e non

b) la componente degli errori è una v.c. non nota e non influenzata dalla sua natura casuale e non

c) la componente degli errori è un parametro non noto e influenzato dalla sua natura casuale e non

d) la componente degli errori è un parametro noto e non influenzato dalla sua natura casuale e non

9. Quando un processo stocastico si dice stazionario in covarianza

a) quando gli autovalori del polinomio matriciale sono maggiori di 1 in valore assoluto

b) quando gli autovalori del polinomio matriciale sono minori di 1 in valore assoluto

c) quando gli autovalori del polinomio matriciale sono uguali a 1 in valore assoluto

d) quando gli autovettori del polinomio matriciale sono minori di 1 in valore assoluto

10. Quali sono i criteri di informazione più comuni

a) Akaike (AIC), Schwarz-Bayesian (BIC)

b) Akaike (AIC), Hannan-Quinn (HQ)

c) Akaike (AIC), Schwarz-Bayesian (BIC) e Hannan-Quinn (HQ)

d) Schwarz-Bayesian (BIC) e Hannan-Quinn (HQ)

11. Quando e perché si usa un modello ARCH

a) quando non si è in presenza di incertezza misurata da una varianza condizionata che varia nel tempo

b) quando si è in presenza di incertezza misurata da una varianza condizionata che non varia nel tempo

c) quando si è in presenza di incertezza misurata da una varianza condizionata che varia nel tempo

d) quando si è in presenza di incertezza misurata da una varianza che varia nel tempo

Domande a risposta aperta

1. Dato un processo stocastico:

a) stabilire quando esso è stazionario in senso debole; b) descrivere la notazione della funzione di autocovarianza tra y_te y_t-k; c) descrivere la notazione della funzione di autocorrelazione tra y_te y_t-k d) descrivere la notazione con cui si spiega perché la funzione di autocorrelazione dipende solo dal lag temporale k e per k=0 è uguale a 1

SOLUZIONE

a) Un processo si dice stazionario in senso debole:

· in media se E(y_t ) = µ < ∞ per t ϵ T(ossia la media è costante ed è finita e non dipende dal parametro t);

· in varianza se E(y_t- µ)² =σ² < ∞ per t ϵ T(ossia la varianza è costante ed è finita e non dipende da t);

· in covarianza se Cov(y_t, y_t-k) = E[(y_t - µ)( y_t-k - µ)] = ϒ_k (ossia le covarianze sono finite e dipendono solo dal ritardo temporale k)

b) la notazione con cui si esprime l’autocovarianza tra y_t e y_t-k è: Cov(y_t, y_t-k) = E[(y_t - µ)( y_t-k - µ)] per t ϵ T e t-k ϵ T; essa dipende soltanto dai ritardi k

c) la notazione con cui si esprime l’autocorrelazione tra y_t e y_t-k è: Cor(y_t, y_t-k) = ϒ_t,t-k/RDQ (σ_t²*σ_t-k²)=ρ_t,t-kper t ϵ T e t-k ϵ T; anche la funzione di autocorrelazione dipende soltanto dai ritardi k

d) ϒ_t,t-k/RDQ (σ_t²*σ_t-k²)= ϒ_t,t-k/RDQ (σ²*σ²)= ϒ_k / ϒ₀= ρ_kovviamente per k=0ρ_k=1

2. Dato un processo stocastico definire gli stimatori e commentarli:

a) valore atteso; b) varianza; c) autocovarianza; d) autocorrelazione

SOLUZIONE

a) valore atteso => µ(stim)=1/n ∑ⁿ_t=1 y_t; esso è uno stimatore corretto del valore atteso ed è legato al tempo;

b) varianza => σ_t²(stim)= ϒ₀=1/n ∑ⁿ_t=1 [y_t- µ(stim)²]; è uno stimatore consistente ma non efficiente legato al tempo

c) autocovarianza => ϒ₀=1/n ∑^n-k_t=1 [y_t- µ(stim)]* [y_t+k- µ(stim)]; è uno stimatore legato ai ritardi k

d) autocorrelazione => ρ_k(stim)= ϒ_k (stim)/ ϒ₀(stim); è uno stimatore legato ai ritardi k

3. Dato un processo stocastico:

a) descrivere brevemente il concetto di diagnostica; b) perché si prende in considerazione il correlogramma dei residui standardizzati; c) quali sono le linee di codice per implementare la diagnostica; d) da cosa si evince che il processo stocastico è stazionario

4. Dato un processo stocastico:

a) descrivere brevemente da cosa è influenzata la autocorrelazione parziale π_ktra dati distanti k lag; b) cosa misura la funzione di autocorrelazione parziale ρ_k ; c) quali sono le linee si utilizzano per calcolarla; d) dato t=7 e K=5 quali come si misura la autocorrelazione tra y_t e y_t-k

SOLUZIONE

a) la funzione di autocorrelazione parziale π_ktra dati distanti k lag è influenzata dalle relazioni lineari con i dati intermedi;

b) la funzione di autocorrelazione parziale π_k misura la correlazione tra y_t e y_t-k dopo che sia stata eliminata la parte che può essere spiegata linearmente composta dai seguenti valori intermedi y_t-1 , y_t-2 ,……..,y_t-k-1

c) le linee di codice per calcolarla sono: library(tseries); y_t ……..; pacf(y_t)

d) la autocorrelazione tra y₇ e y_7-5è misurata eliminando i seguenti valori intermedi : y_7-1 , y_7-2, y_7-3, y_7-5+1;

y₆ , y₅, y₄, y₃

5. Dato un processo stocastico white noise:

a) descrivere brevemente se il processo stocastico è stazionario; b) descrivere brevemente se il processo stocastico presenta una correlazione fra le v.c.; c) quando si definisce gaussiano; d) quali sono le caratteristiche

SOLUZIONE

a) il processo stocastico white noise è stazionario in senso debole ma non lo è in senso forte;

b) il processo stocastico white noise prevede l’assenza di correlazione fra le v.c.

c) si definisce gaussiano quando se le v.c. si distribuiscono seconda una normale

d) le caratteristiche sono che il valore atteso è uguale a 0 per tutti i valori di t ricompresi in T, che la varianza è omoschedastica, che la covarianza tra le variabile distanti k lags, per qualsiasi valore di k è uguale a 0